题目背景

帆帆不满足于只构建一棵深蓝之树，他觉得深蓝之树只有深蓝色太单调了，于是想给这棵树染上颜色。

题目描述

由于现在已经来到了魔幻的龙年，帆帆的深蓝之树已经被染上了颜色，结点 $i$ 的颜色为 $a_i$。

帆帆是一个喜新厌旧的人，在接下来的 $q$ 天中，他每天都会改变他喜欢的颜色，第 $i$ 天他喜欢的两种颜色是 $x_i,y_i$（$x_i\neq y_i$）。

但是为了照顾自己的树，他需要经常在树上移动，并且只会经过自己喜欢的颜色。

具体来说，第 $i$ 天，帆帆会选择一个有序结点对 $(u,v)$，然后沿着 $u\to v$ 的唯一简单路径移动，并且中间经过的结点（包含 $u,v$）颜色必须 $\in \{x_i,y_i\}$（$u$ 可以等于 $v$），之后可以抽取一次宵宫。

每一天你都需要抽取一个满命宵宫，然后告诉帆帆有多少种可能的选择有序结点对的方案。

输入格式

第一行两个正整数 $n,q$。

接下来一行 $n$ 个正整数 $a_1,a_2,\cdots,a_n$ 表示每个点的颜色。

接下来一行 $n-1$ 个正整数 $p_2,p_3,\cdots,p_n$，表示对所有 $2\le i\le n$，树上存在一条边 $(p_i,i)$。

接下来 $q$ 行，每行两个正整数 $x_i,y_i$。

输出格式

对于每组询问输出一行一个正整数表示答案。

5 3
1 2 1 3 3
1 1 2 2
1 2
1 3
2 3

9
6
9

提示

【样例 $1$ 解释】

树的形态如图所示：

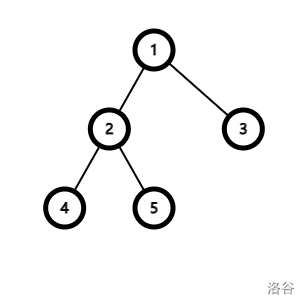
对于第一组询问，合法的路径有且仅有 $\{1,2,3\}$ 中一点到另一点的路径。

对于第二组询问，合法的路径有且仅有 $1\to 1,1\to 3,3\to 1,3\to 3,4\to 4,5\to 5$。

【子任务约束】

本题采用子任务捆绑测试。

对于 $100\%$ 的数据，有 $1\le n\le 10^6$，$1\le q\le 2\times 10^6$，$1\le a_i,x,y\le n$，$x\neq y$。保证 $p_i<i$。

子任务编号	$n$	$q$	特殊性质	分值	依赖子任务
Subtask #1	$\le 100$		无	$7$	无
Subtask #2	$\le 2000$			$18$	$1$
Subtask #3	$\le 10^5$	$\le 2\times 10^5$	A	$5$	无
Subtask #4			B	$19$
Subtask #5			无	$21$	$1,2,3,4$
Subtask #6	$\le 2\times 10^5$	$\le 5\times 10^5$		$10$	$5$
Subtask #7	$\le 10^6$	$\le 2\times 10^6$		$20$	$6$

特殊性质 A：$p_i=1$。

特殊性质 B：$p_i=i-1$。