题目描述

给定一个 $n\times n$ 的矩形，其中从左上角开始，对角线上连续的 $k$ 个格子中有障碍物。你可以把若干 $1\times2$ 的小矩形放置到该大矩形中，要求是放置的两个小矩形不能占据相同的格子，且不能碰到障碍物。例如下图是 $n=4,k=2$ 的例子，我们放置了 $6$ 个 $1\times2$ 的小矩形。

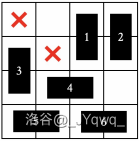
给定 $n,k$，请你输出一个方案，使得放置的 $1\times2$ 小矩形尽可能多。可以证明，$n=4,k=2$ 时，至多只能放置 $6$ 个小矩形。

输入格式

输入一行两个用空格分隔的正整数 $n,k$，表示矩形的大小和障碍物的数量。

输出格式

输出 $n$ 行，每行 $n$ 个整数（用任意数量的空格分隔）。放置的小矩形分别用 $1,2,\cdots$ 编号。不放置小矩形的格子输出 $0$。如有多种最优方案（放置最多数量的小矩形），输出任意一种即可。

4 2

0 0 1 2
3 0 1 2
3 4 4 0
5 5 6 6

5 3

0 8 8 9 10
1 0 0 9 10
1 3 0 0 7
2 3 5 5 7
2 4 4 6 6

提示

对于 $50\%$ 的测试数据，有 $1\le k\le n\le10$。

对于 $100\%$ 的测试数据，有 $1\le k\le n\le50$。

本题原始满分为 $20\text{pts}$。