#B3740. [信息与未来 2018] 棋盘游戏
[信息与未来 2018] 棋盘游戏
Description
给定一个十进制数 ,将它转换为二进制字符串并在高位填 以补足 位,就得到了 一个长度为 的 字符串,我们用这个字符串表示 的棋盘,按从左到右、从上到下的顺序将 (白子)、(黑子)放入棋盘。
例如,,按顺序填入棋盘( 白子、 黑子),得到如下棋盘(左边棋盘):
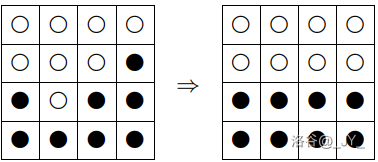
我们现在可以交换棋盘中相邻(共享一条边的两个格子相邻,因此一个格子至多有 个相邻的格子)的黑色和白色棋子。从左图的棋盘变为全部白子在上、全部黑子在下(右边棋盘所示)的棋盘,至少需要 步。
对于给定的棋盘(保证棋盘中恰好有 个白子和 个黑子),求把棋盘变为全部白子在上、全部黑子在下最少的交换步数。
Input Format
输入一行一个整数 ,为十进制表示下的棋盘。
Output Format
输出一行一个整数,最少需要交换的步数。
447
3
42405
8
Hint
样例解释
样例
参考上图,将 处的⿊⼦移动到 需要 步。
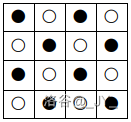
样例
如下图所示,。
数据规模
的测试数据满足棋盘可以在 次交换内变为白子在上、黑子在下。
所有数据保证 ,且 转换为二进制后恰好有 个 。
本题原始满分为 。

 京公网安备 11011102002149号
京公网安备 11011102002149号