Description

给定 $n$ 个不同的单词及其出现的频次，请你构造一种哈夫曼编码（Huffman Coding）方案。

哈夫曼编码是一种可变长前缀编码，它通过构建哈夫曼树来实现，使得所有单词的编码长度与其频次的乘积之和（即带权路径长度，WPL）最小。在哈夫曼树中，左分支通常代表 $0$，右分支通常代表 $1$。

由于构建哈夫曼树时，对于权值相同的节点合并顺序不同，以及左右子树的分配不同，可能会产生多种满足条件的编码方案。本题只需输出任意一种合法的哈夫曼编码方案即可。输出的单词顺序应与输入顺序保持一致。

Input Format

第一行包含一个正整数 $n$，表示单词的个数。

接下来 $n$ 行，每行包含一个由小写英文字母组成的非空字符串 $s_i$ 和一个正整数 $w_i$，分别表示第 $i$ 个单词及其出现的频次。

Output Format

输出共 $n$ 行。

每行输出一个字符串和一个 $01$ 字符串，中间以一个空格隔开，分别表示单词 $s_i$ 及其对应的哈夫曼编码。

输出的单词顺序应与输入顺序保持一致。

4
a 1
b 2
c 3
d 4

a 110
b 111
c 10
d 0

6
algorithm 10
complexity 5
structure 2
optimization 23
graph 7
tree 15

algorithm 00
complexity 0111
structure 0110
optimization 11
graph 010
tree 10

Hint

样例 1 解释

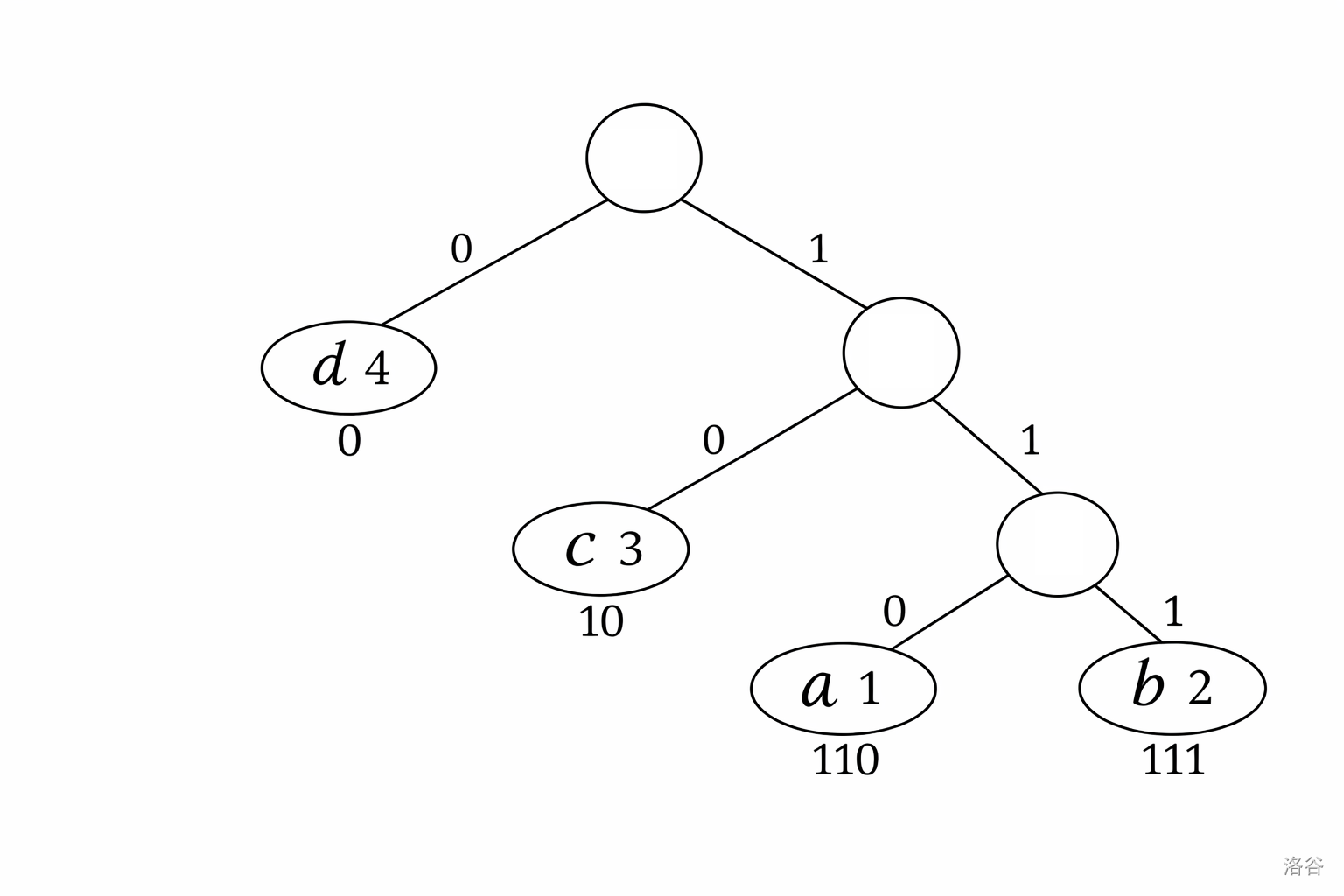
对于第一组数据，一种构建过程如下：

1. 取出频次最小的 $\tt a$（$1$）和 $\tt b$（$2$），合并为一个新节点，权值为 $1+2=3$。
2. 当前权值集合为 $\{3, 3, 4\}$（其中第一个 $3$ 为新节点，第二个 $3$ 为 $\tt c$）。
3. 取出最小的 $\tt c$（$3$）和新节点（$3$），合并为一个新节点，权值为 $3+3=6$。
4. 当前权值集合为 $\{4, 6\}$。
5. 取出 $\tt d$（$4$）和新节点（$6$），合并为根节点，权值为 $4+6=10$。

假设每次合并时，权值较小的节点作为左子树（标记为 $0$），权值较大的节点作为右子树（标记为 $1$）；若权值相同，则任意分配。 对于上述构建的一种可能树结构：

• $\tt d$ 位于根节点的左侧（编码 $0$）。
• $\tt c$ 位于根节点 $\to$ 右节点 $\to$ 左节点（编码 $10$）。
• $\tt a$ 位于根节点 $\to$ 右节点 $\to$ 右节点 $\to$ 左节点（编码 $110$）。
• $\tt b$ 位于根节点 $\to$ 右节点 $\to$ 右节点 $\to$ 右节点（编码 $111$）。

带权路径长度 $\text{WPL} = 4 \times 1 + 3 \times 2 + 1 \times 3 + 2 \times 3 = 19$，这是理论最小值。其他满足 WPL 最小的编码方案也被视为正确答案。

:::align{center} :::

数据范围

对于 $100\%$ 的数据，满足 $1 \le n \le 1000$，字符串 $s_i$ 的长度不超过 $20$，且 $1 \le w_i \le 10^9$。保证所有字符串 $s_i$ 互不相同。