该比赛已结束，您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。

附加文件

题目描述

你没有看错，这又是一道线段树题。

在这道题中，你会得到一个广义线段树，然后对其进行一些复杂度分析。

广义线段树是一棵大小为 $2n - 1$ 的、有恰好 $n$ 个叶子节点的二叉树。

将这 $n$ 个叶子节点按照先序遍历的顺序排列，则第 $i$ 个叶子节点代表的区间是 $[i, i]$。

在此基础上：

• 对于一个非叶子节点
• 若其左儿子代表区间为 $[L_a, R_a]$，右儿子代表区间为 $[L_b, R_b]$
• 不难发现 $R_a + 1 = L_b$
• 则该节点代表的区间为 $[L_a, R_b]$

此时定义这个非叶子节点 $x$ 的分割位置为：$mid(x) = R_a$

下面给出在线段树上进行区间操作的伪代码：

function F(x, l, r, Fl, Fr)
    if Fl ≤ l and Fr ≥ r then
        Do Something
        return
    end if
    Do Something
    if Fl ≤ mid(x) then
        F(Lson(x), l, mid(x), Fl, Fr)
    end if
    if Fr > mid(x) then
        F(Rson(x), mid(x) + 1, r, Fl, Fr)
    end if
    Do Something
end function

当你需要对区间 $[Fl, Fr]$ 进行操作时，你会调用 F(Root, 1, n, Fl, Fr)，其中 Root 代表线段树的根节点。

再定义 $G(l, r)$ 表示调用 F(Root, 1, n, l, r) 后，函数 F 被调用的总次数（初始调用也计入）。

现在你手上有一棵广义线段树。

你需要对于所有 $i \in [1, 2n - 1]$ 求出满足：$1 \le l \le r \le n,\quad G(l, r) = i$ 的数对 $(l, r)$ 的数量。

输入格式

第一行一个整数 $n$。

第二行 $n - 1$ 个整数，按照先序遍历的顺序，给出每个非叶子节点 $x$ 的分割位置 $mid(x)$。

保证给定的 $n - 1$ 个整数是一个排列。

不难发现，通过这些信息可以唯一确定一棵广义线段树。

输出格式

一行 $2n - 1$ 个整数，第 $i$ 个整数表示满足 $1 ≤ l ≤ r ≤ n$ 且 $G(l, r) = i$ 的数对数量。

样例

样例输入 1

6
5 1 3 2 4

样例输出 1

1 2 2 3 6 4 3 0 0 0 0

样例解释 1

样例 1 中给出的线段树如下图：

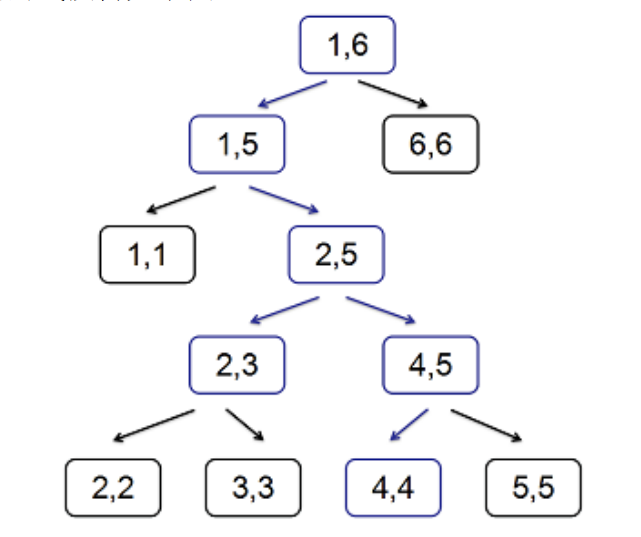
例如，调用：F(Root, 1, 6, 2, 4) 会对图中所有蓝色节点调用一次函数，因此：$G(2, 4) = 6$。

数据范围与提示

本题共 $10$ 个测试点，每个测试点分值为 $10$。

测试点具体限制如下：

• 测试点 1：$n \le 500$
• 测试点 2, 3：$n \le 5000$
• 测试点 4, 5：数据生成方式为，从根节点开始，若该非叶子节点代表区间为 $[l, r]$，则在 $[l, r − 1]$ 之间等概率随机一个整数作为这个节点的分割位置，然后用同样的方法 生成该节点的左右子树。
• 测试点 6, 7：对于根节点左子树中的所有非叶子节点，若其代表区间为 $[l, r]$，那么其 $mid$ 值为 $r − 1$，对于根节点右子树中的所有非叶子节点，若其代表区间为 $[l, r]$，那么其 $mid$ 值为 $l$
• 测试点 8, 9, 10：无特殊限制。
• 所有数据满足：$1 \le n \le 100000$