标题来自：Pale - MIMI

题目描述

有一棵 $n$ 个结点的树，每个点有点权 $a_i$。

现在云浅会进行 $q$ 次询问，第 $i$ 次询问给出树上的 $k_i$ 条边，如果断掉这 $k_i$ 条边，那么树会分裂成 $k_i+1$ 个连通块。你需要对每个连通块 $P$ 找到一个点 $u$，使得 $\sum_{v\in P}\text{dist}(u,v)\times a_v$ 最小。这里 $\text{dist}(u,v)$ 指的是树上 $u,v$ 两点之间最短路径上的边数。如果有多个，取编号最小的那个。

这里询问之间互相独立，也就是说并没有真的断掉这些边。

输入格式

本题有多组数据。

第一行一个正整数 $T$ 表示数据组数。对于每组数据：

第一行两个正整数 $n,q$。

接下来一行 $n$ 个正整数表示 $a_1,a_2,\cdots,a_n$。

接下来 $n-1$ 行，每行两个正整数 $u,v$ 表示树上的一条边。

接下来 $q$ 行每行先输入一个正整数 $k_i$ 表示这次询问断掉的边数，接下来输入 $k_i$ 个 $[1,n-1]$ 中的正整数 $p_1,p_2,\cdots,p_{k_i}$ 表示断掉输入的第 $p_1,p_2,\cdots,p_{k_i}$ 条边。

输出格式

对于每组询问，假设你找到的 $k_i+1$ 个点的编号分别为 $x_1,x_2,\cdots,x_{k_i+1}$，你需要先把 $x$ 升序排序，然后输出

$$\left(\sum_{i=1}^{k_i+1}528221^{i-1}\times x_i\right)\bmod 2^{32} $$

的值。

样例 $1$ 输入

2
5 7
1 1 1 1 1
4 5
3 2
4 3
3 1
3 4 1 3
1 4
2 4 1
1 3
3 4 2 1
4 4 2 3 1
3 2 3 4
8 5
7 2 8 8 2 1 2 3
1 2
3 7
7 5
7 4
5 8
4 6
3 1
6 5 2 7 4 1 3
2 2 5
3 6 2 3
1 3
7 3 1 2 7 4 5 6

样例 $1$ 输出

1413104888
1584664
3519304965
2112887
1568554287
565816639
2020778538
3477803906
3053484989
4041557075
4225771
3032800292

样例 $1$ 解释

实际上的答案为

1 2 4 5
1 3
1 3 5
3 4
1 2 3 5
1 2 3 4 5
1 2 3 4
1 2 3 4 5 7 8
1 4 8
1 4 6 8
3 8
1 2 3 4 5 6 7 8

以第一组数据的第三组询问为例：以下分别为原本的树和断掉边之后的树。

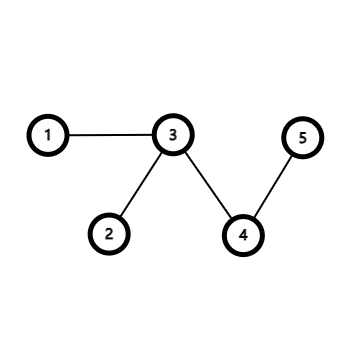
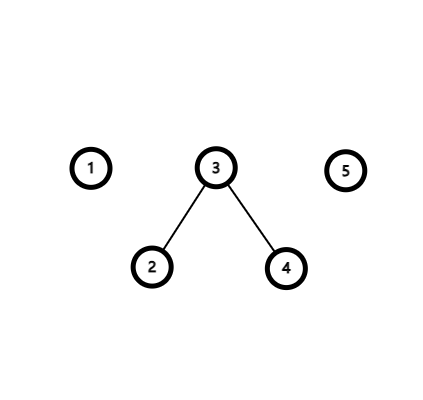
断掉边后图中有三个连通块：$\{1\},\{2,3,4\},\{5\}$，取的最优点分别为 $1,3,5$，按升序输出为 1 3 5。

测试点约束

对于所有数据：$1\le n,q,\sum k_i\le 2\times 10^5,1\le T\le 10,1\le a_i\le 10^4,1\le k_i\le n-1$。

这里和以下表格中的 $\sum k_i$ 指的都是单组数据中 $k_i$ 的和，并非 $T$ 组数据全部的 $k_i$ 之和。

子任务编号	$n\le$	$q,\sum k_i\le$	特殊性质	依赖子任务	分值
Subtask #1	$20$	$2\times 10^5$	$k_i\le 10$	无	$12$
Subtask #2	$500$			$1$	$10$
Subtask #3	$5000$			$1,2$	$11$
Subtask #4	$10^5$		保证输入的第 $i$ 条边为 $(i,i+1)$	无	$15$
Subtask #5			保证 $a_i=1$		$21$
Subtask #6	$2\times 10^5$		无	$1,2,3,4,5$	$31$