题目描述

未来的城市可以抽象成有 $n$ 个点和 $m$ 条边的无向图，可能存在重边自环，每条边有长度 $w_i$。而未来的人们的工作地点都在 $1,2$ 号点（保证 $1,2$ 号点均与其他所有点联通）。

你现在要在这个城市定居了，你选择了在点 $n+1$ 处建立一座新房子。你需要到城市中去，因此你要修几条道路连接你的房子与其他点，使得从你的房子出发可以到达城市中的任意点。而且你掌握未来科技，因此你修的路长度不必是整数，但一定是非负数。

未来的人们都追求效率，他们出行都希望走的越少越好。但是你追求安静祥和的生活，因此你的房子设置了禁令不允许任何外人经过。所以如果你修完路之后他们发现存在某个编号小于 $n+1$ 的点到 $1$ 号或 $2$ 号点的所有最短路都要经过你的房子，他们就会对此禁令感到愤怒！

为了防止他们因为愤怒而攻击你，请明智的选择修路方案，当然你也希望自己出行时走的越少越好，因此你还要使修完路后新房子到其他每个点的最短路长度的总和尽可能小。

本题多测。

输入格式

第一行一个整数 $T$，表示数据组数。

对于每一组数据而言，第一行两个整数 $n,m$。

接下来 $m$ 行，每行三个整数 $u_i,v_i,w_i$，表示 $u_i,v_i$ 之间有一条长 $w_i$ 的边。

输出格式

共 $T$ 行，每行一个整数表示满足上述条件的情况下，最小的长度总和。

如果结果是整数，你只需要输出这个整数，如果是小数，那么你应当保证没有多余的 $0$。

样例1

1
4 4
1 3 1
1 2 2
1 4 4
4 2 3

7

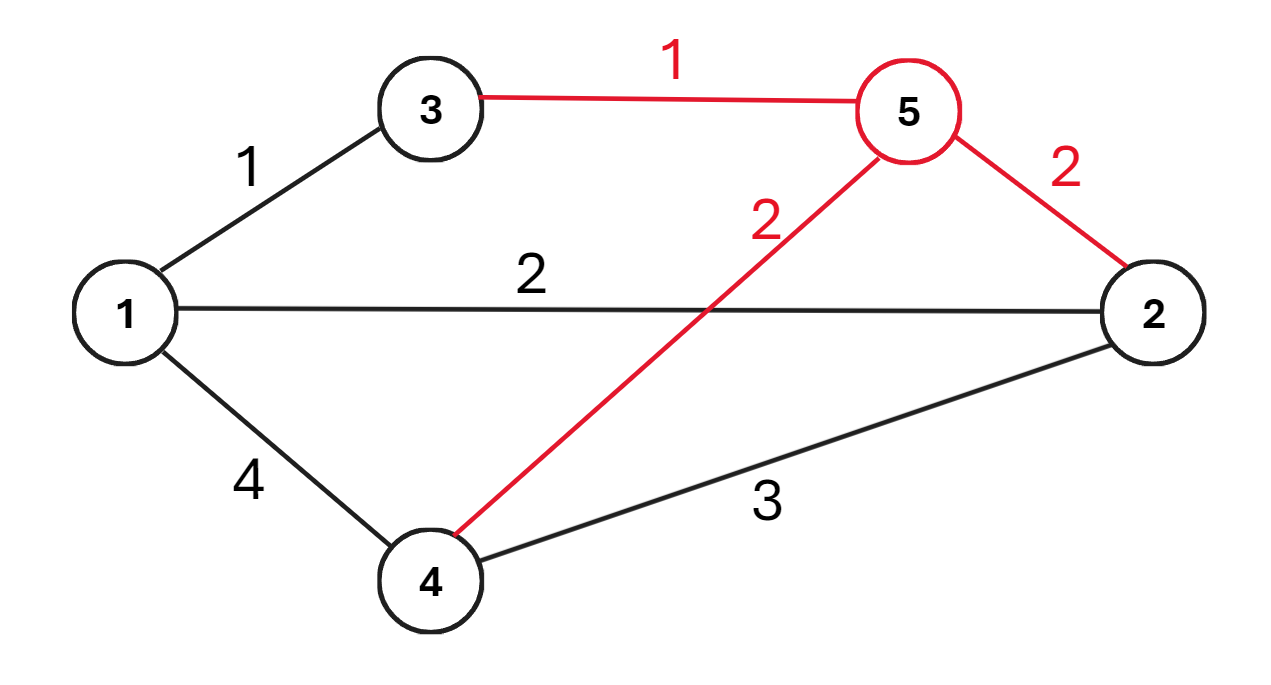如图代表一种可行的方案，红色点代表你的房子，红色边代表你修的路，可以证明，此时你到其他每个点的最短路长度总和是最小的。

值得注意的是，$3$ 号点到 $2$ 号点有两条长度为 $3$ 的最短路，分别是 $3\rightarrow1\rightarrow2$ 和 $3\rightarrow5\rightarrow2$。由于人们可以选择走前一条路而不必经过你的房子，因此他们并不会感到愤怒。

数据范围