题目描述

给定一个包含 $n$ 个结点和 $m$ 条带权边的有向图，求所有点对间的最短路径长度，一条路径的长度定义为这条路径上所有边的权值和。

注意：

1. 边权可能为负，且图中可能存在重边和自环；

2. 部分数据卡 $n$ 轮 SPFA 算法。

输入格式

第 $1$ 行：$2$ 个整数 $n,m$，表示给定有向图的结点数量和有向边数量。

接下来 $m$ 行：每行 $3$ 个整数 $u,v,w$，表示有一条权值为 $w$ 的有向边从编号为 $u$ 的结点连向编号为 $v$ 的结点。

输出格式

若图中存在负环，输出仅一行 $-1$。

若图中不存在负环：

输出 $n$ 行：令 $dis_{i,j}$ 为从 $i$ 到 $j$ 的最短路，在第 $i$ 行输出 $\sum\limits_{j=1}^n j\times dis_{i,j}$，注意这个结果可能超过 int 存储范围。

如果不存在从 $i$ 到 $j$ 的路径，则 $dis_{i,j}=10^9$；如果 $i=j$，则 $dis_{i,j}=0$。

5 7
1 2 4
1 4 10
2 3 7
4 5 3
4 2 -2
3 4 -3
5 3 4

128
1000000072
999999978
1000000026
1000000014

5 5
1 2 4
3 4 9
3 4 -3
4 5 3
5 3 -2

-1

提示

【样例解释】

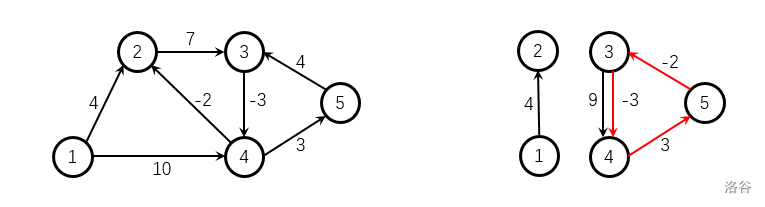
左图为样例 $1$ 给出的有向图，最短路构成的答案矩阵为：

0 4 11 8 11 
1000000000 0 7 4 7 
1000000000 -5 0 -3 0 
1000000000 -2 5 0 3 
1000000000 -1 4 1 0 

右图为样例 $2$ 给出的有向图，红色标注的边构成了负环，注意给出的图不一定连通。

【数据范围】

对于 $100\%$ 的数据，$1\leq n\leq 3\times 10^3,\ \ 1\leq m\leq 6\times 10^3,\ \ 1\leq u,v\leq n,\ \ -3\times 10^5\leq w\leq 3\times 10^5$。

对于 $20\%$ 的数据，$1\leq n\leq 100$，不存在负环（可用于验证 Floyd 正确性）

对于另外 $20\%$ 的数据，$w\ge 0$（可用于验证 Dijkstra 正确性）

upd. 添加一组 Hack 数据：针对 SPFA 的 SLF 优化