#P3779. [SDOI2017] 龙与地下城
[SDOI2017] 龙与地下城
题目描述
小Q同学是一个热爱学习的人,但是他最近沉迷于各种游戏,龙与地下城就是其中之一。
在这个游戏中,很多场合需要通过掷骰子来产生随机数,并由此决定角色未来的命运,因此骰子堪称该游戏的标志性道具。
骰子也分为许多种类,比如4面骰、6面骰、8面骰、12面骰、20面骰,其中20面骰用到的机会非常多。当然,现在科技发达,可以用一个随机数生成器来取代真实的骰子,所以这里认为骰子就是一个随机数生成器。
在战斗中,骰子主要用来决定角色的攻击是否命中,以及命中后造成的伤害值。举个例子,假设现在已经确定能够命中敌人,那么(也就是掷出个面骰子之后所有骰子显示的数字之和)就是对敌人的基础伤害。在敌人没有防御的情况下,这个基础伤害就是真实伤害。
众所周知,骰子显示每个数的概率应该是相等的,也就是说,对于一个面骰子,显示中每一个数字的概率都是 。
更形式地说,这个骰子显示的数满足离散的均匀分布,其分布列为

除此之外还有一些性质
-
的一阶原点矩(期望)为
-
的二阶中心矩(方差)为$\mu_2(W)=E((W-E(W))^2)=\sum_{i=0}^{X-1}(i-E(W))^2P(W=i)=\frac {X^2-1}{12}$
言归正传,现在小Q同学面对着一个生命值为A的没有防御的敌人,能够发动一次必中的攻击,显然只有造成的伤害不少于敌人的生命值才能打倒敌人。但是另一方面,小Q同学作为强迫症患者,不希望出现overkill,也就是造成的伤害大于的情况,因此只有在打倒敌人并且不发生overkill的情况下小Q同学才会认为取得了属于他的胜利。
因为小Q同学非常谨慎,他会进行10次模拟战,每次给出敌人的生命值以及overkill的标准,他想知道此时取得属于他的胜利的概率是多少,你能帮帮他吗?
输入格式
第一行是一个正整数,表示测试数据的组数,
对于每组测试数据:
第一行是两个整数 , ,分别表示骰子的面数以及骰子的个数;
接下来10行,每行包含两个整数 , ,分别表示敌人的生命值以及overkill的标准。
输出格式
对于每组测试数据,输出10行,对每个询问输出一个实数,要求绝对误差不超过,
也就是说,记输出为,答案为,若满足,则认为输出是正确的。
1
2 19
0 0
0 1
0 2
0 3
0 4
0 5
0 6
0 7
0 8
0 9
0.000002
0.000038
0.000364
0.002213
0.009605
0.031784
0.083534
0.179642
0.323803
0.500000
提示
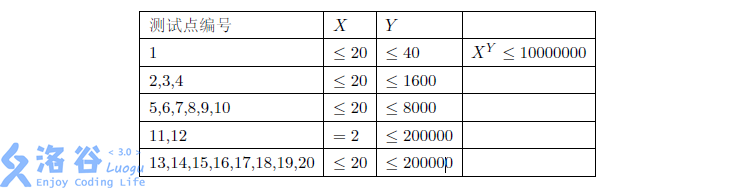
对于的数据,,,,,保证满足的数据不超过组。

 京公网安备 11011102002149号
京公网安备 11011102002149号