Description

据说，加勒比海盗每次抢劫完，如果有金银珠宝等贵重物品，都会以特殊的仪式分宝。他们首先将珠宝装在一个个

边长为1的土陶立方体中，并在盖子上标记出珠宝的价值v。然后将这些盒子排列成一个长为l，宽为w的矩形（如果

珠宝不够，可能会用空的土陶盒占据空位，并在盖子上标记价值为0），第i行第j列的土陶盒上标记的价值为vij(

其中0<i<=w,0<j<=l,左下角的土陶盒所在位置为第一行第一列)。海盗们按照功劳的大小，决定分宝的顺序，被轮

到选取珠宝的海盗将被发给一个底面为m×n的矩形，高为h的木箱子，并要求用这个木箱子来装所选土陶盒，最后

盖上木箱盖子。土陶盒的选取需要分批选取，要求每批土陶盒为一个等同于木箱底面的紧挨着的矩形区域，且木箱

长为m的边必须与土陶盒摆成矩形时长为w的边平行。被选走的土陶盒所在位置在被选走后马上由空土陶盒填充。海

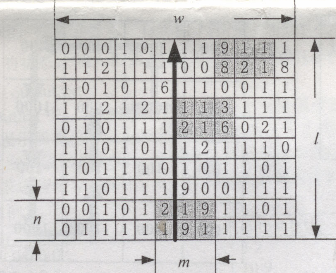
盗从土陶盒摆成的矩形底部正中出发，即从第一行的第w/2(取下整)列的土陶盒的右下角出发，向上沿着据土陶盒

摆成的矩形区域的最左边w/2（取下整）的直线前进。如图中粗线箭头所示。设第k批被选取的区域的最小角为第i[

k]行第j[k]列的土陶盒，jk必须满足(m/2+j[k]-w/2)（整个表达式取下整）<=a，其中k>=1,且当j[k]=j[k-1]的时

候,i[k]必须满足i[k]-i[k-1]>=d1,当j[k]!=j[k-1]时,i[k]必须满足i[k]-i[k-1]>=d2，其中k>=2.

Input

第一行包括8个正整数，这些正整数之间用一个空格隔开，

这8个正整数依次为l，w，m，n，h，a，d1，d2。

从第二行到第l+1行，每行有w个整数，

不妨将输入文件中第i+1行，第j列的整数记做vij（1<=j<=w，1<=i<=l），

分别表示土陶盒上标记的珠宝价值，同一行的整数之间用一个空格隔开。

1<=l<=2000，1<=w<=2000，1<=m<=200，1<=n<=200，1<=h<=20，1<=a<=2000，1<=d1<=2000，1<=d2<=2000，0<=vij<=255。

需注意的是：

输入时vij是从左上角的土陶盒开始，但在求解时左下角的那个土陶盒为第1行第1列的土陶盒。

Output

输出文件中的第一行为两个整数，分别是最多能得到的珠宝总价值Total

Samples

10 12 3 2 3 5 2 3
0 0 0 1 0 1 1 1 9 1 1 1
1 1 2 1 1 1 0 0 8 2 1 8
1 0 1 0 1 6 1 1 0 0 1 1
1 1 2 1 2 1 1 1 3 1 1 1
0 1 0 1 1 1 2 1 6 0 2 1
1 1 0 1 0 1 1 2 1 1 1 0
1 0 1 1 1 0 1 0 1 1 0 1
1 1 0 1 1 1 9 0 0 1 1 1
0 0 1 0 1 2 1 9 1 1 0 1
0 1 1 1 1 1 9 1 1 1 1 1

59

Limitation

数据保证d1,d2>=n