You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.

题目描述

CSP-J 2025 第二轮正在进行。小 R 所在的考场共有 $n \times m$ 名考生，其中所有考生的 CSP-J 2025 第一轮成绩互不相同。所有 $n \times m$ 名考生将按照 CSP-J 2025 第一轮的成绩，由高到低蛇形分配座位，排列成 $n$ 行 $m$ 列。具体地，设小 R 所在的考场的所有考生的成绩从高到低分别为 $s_1 > s_2 > \dots > s_{n \times m}$，则成绩为 $s_1$ 的考生的座位为第 1 列第 $1$ 行，成绩为 $s_2$ 的考生的座位为第 $1$ 列第 $2$ 行，$\dots$，成绩为 $s_n$ 的考生的座位为第 $1$ 列第 $n$ 行，成绩为 $s_{n+1}$ 的考生的座位为第 $2$ 列第 $n$ 行，$\dots$，成绩为 $s_{2n}$ 的考生的座位为第 $2$ 列第 $1$ 行，成绩为 $s_{2n+1}$ 的考生的座位为第 $3$ 列第 $1$ 行，以此类推。

例如，若 $n = 4, m = 5$，则所有 $4 \times 5 = 20$ 名考生将按照 CSP-J 2025 第一轮成绩从高到低的顺序，根据下图中的箭头顺序分配座位。

:::align{center} :::

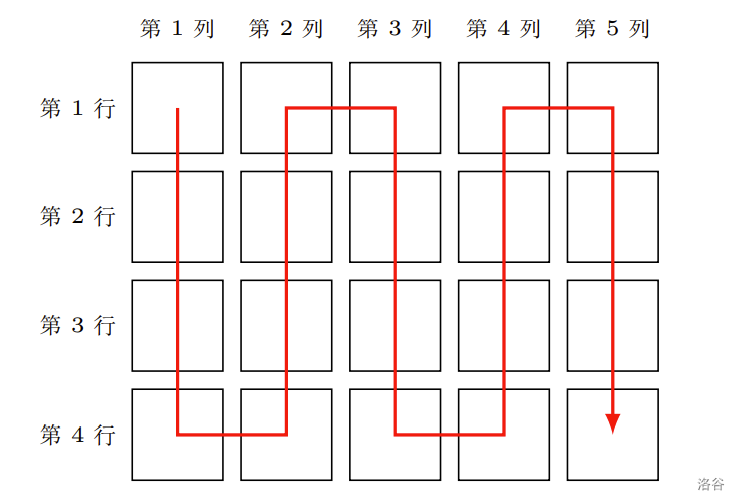给定小 R 所在的考场座位的行数 $n$ 与列数 $m$，以及小 R 所在的考场的所有考生 CSP-J 2025 第一轮的成绩 $a_1, a_2, \dots, a_{n \times m}$，其中 $a_1$ 为小 R CSP-J 2025 第一轮的成绩，你需要帮助小 R 求出，他的座位为第几列第几行。

输入格式

输入的第一行包含两个正整数 $n, m$，分别表示小 R 所在的考场座位的行数与列数。

输入的第二行包含 $n \times m$ 个正整数 $a_1, a_2, \dots, a_{n \times m}$，分别表示小 R 所在的考场的所有考生 CSP-J 2025 第一轮的成绩，其中 $a_1$ 为小 R CSP-J 2025 第一轮的成绩。

输出格式

输出一行两个正整数 $c, r$，表示小 R 的座位为第 $c$ 列第 $r$ 行。

输入输出样例 #1

输入 #1

2 2
99 100 97 98

输出 #1

1 2

输入输出样例 #2

输入 #2

2 2
98 99 100 97

输出 #2

2 2

输入输出样例 #3

输入 #3

3 3
94 95 96 97 98 99 100 93 92

输出 #3

3 1

说明/提示

【样例 1 解释】

按照成绩从高到低的顺序，成绩为 $100$ 的考生的座位为第 $1$ 列第 $1$ 行，成绩为 $99$ 的考生的座位为第 $1$ 列第 $2$ 行，成绩为 $98$ 的考生的座位为第 $2$ 列第 $2$ 行，成绩为 $97$ 的考生的座位为第 $2$ 列第 $1$ 行。小 R 的成绩为 $99$，因此座位为第 $1$ 列第 $2$ 行。

【样例 2 解释】

按照成绩从高到低的顺序，成绩为 $100$ 的考生的座位为第 $1$ 列第 $1$ 行，成绩为 $99$ 的考生的座位为第 $1$ 列第 $2$ 行，成绩为 $98$ 的考生的座位为第 $2$ 列第 $2$ 行，成绩为 $97$ 的考生的座位为第 $2$ 列第 $1$ 行。小 R 的成绩为 $98$，因此座位为第 $2$ 列第 $2$ 行。

【数据范围】

对于所有测试数据，保证：

• $1 \leq n \leq 10$, $1 \leq m \leq 10$;
• 对于所有 $1 \leq i \leq n \times m$，均有 $1 \leq a_i \leq 100$，且 $a_1, a_2, \dots, a_{n \times m}$ 互不相同。

::cute-table{tuack}

特殊性质 A：对于所有 $1 \leq i \leq n \times m$，均有 $a_i = i$。

特殊性质 B：对于所有 $1 \leq i \leq n \times m$，均有 $a_i = n \times m - i + 1$。