Description

南非世界杯离我们越来越近了，与足球有紧密联系的足球彩票也越来越引起了人们的强烈关注。

了解足球彩票的人可能知道，足球彩票中有一种游戏叫做“胜负彩”，意为猜比赛的胜负。下面是一些与胜负彩有关的术语：

**注      ** ：每一组有效组合数据。

 **投    注** ：彩民以现金购买足球彩票的行为。

单式投注 ：彩民对于所有球队的比赛成绩均只选择一种预测结果的投注方式。投注的数量（注数）为1。

复式投注 ：彩民对于某些场次的比赛成绩选择两种以上的预测结果的投注方式。投注的数量为复式投注的组合数。例如，某彩民对一场比赛预测了两个结果（例如，胜平），另一场比赛预测了三个结果（胜负平），其他比赛都只预测了一种结果，那么注数就是2×3 = 6。这样的一个复式投注，可以看成一个包含六种单式投注的集合。

胜负彩的玩法一般是这样的。彩票机构指定一轮比赛中的若干场，让彩民去猜每场比赛的结果（胜、负、平）。根据彩民猜中比赛的场次，来确定中奖的额度。

我们现在考虑一个简化的模型。对于一轮比赛，彩民需要竞猜其中n场比赛的结果，每场比赛的胜负平都有一个概率 p ( i , r )。其中，i表示第i场比赛。r = 0, 1, 2，分别表示比赛结果的（主队）负、平、胜。 p ( i , r )则表示第i场比赛、结果为r的概率。此外，还有一个概率 q ( i , r )，表示第i场比赛，投注购买结果为r的概率。

例如，如果 q (1,0) = 0.5，我们可以知道第一场比赛有50%的投注会买主队输球。我们假设这n场比赛互不相关，即 p ( i , r )的结果不会受 p ( j , r’)的影响， q ( i , r )的结果也不会受 q ( j , r’)的影响（r ≠ r’）。

在这个模型里，我们规定，必须猜中全部*n*场比赛的结果才能获奖。总奖金为 *M* ，由所有获奖的投注平分。**因此，对于一个单式投注*R~i~* = {*r~i~* ~1~ , *r~i~* ~2~ , ** **…**  **,  *r~in~* }** **，*r~ij~***表示投注*R~i~*对第*j*场比赛的预测结果，它的中奖概率为：

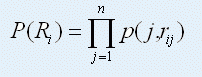
设投注总数为 N ，那么中奖的投注总数为：

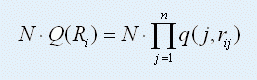
于是，投注*R~i~*所能得到的奖金的期望（平均意义下能够获得的奖金数）就是：

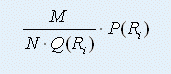
以上考虑的仅仅是单式投注的情况，即仅考虑单注*R~i~*的中奖情况。对于复式投注，情况要复杂一些。采用复式投注时，投注的是一个集合*R* = {*R* ~1~ , *R* ~2~ , …,  *R~k~* }，其中*k*是投注的数量。例如，三场比赛，第一场猜“胜负”，第二场猜“平”，第三场猜“负平”，则*k* = 4，*R*集合如下：

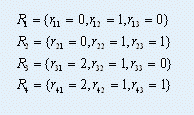
复式投注R中，只要有一个R~i~猜对所有比赛结果，即可中奖。因此，复式投注R所能获得的奖金的期望就是：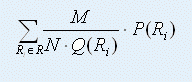

我们的问题是，给定n场比赛的信息（胜负平的概率和彩民购买三种结果的概率），以及复式投注中可以购买的最大注数 U ，要求设计一种复式投注的方案，在不超过最大注数（复式投注的注数k ≤ U）的前提下，使得获得奖金的期望最大。

Format

Input

第一行四个整数 n, N, M, U （ n , U ≤ 10 ^4^ , N , M ≤ 10^9^）。

以下*n*行，每行六个实数。第*i* + 1行的六个实数为 *p* ( *i* , 0),  *p* ( *i* , 1),  *p* ( *i* , 2),  *q* ( *i* , 0),  *q* ( *i* , 1)和 *q* ( *i* , 2)，用来描述第*i*场比赛的相关信息。其中， *p* ( *i* , 0) +  *p* ( *i* , 1) +  *p* ( *i* , 2) = 1,  *q* ( *i* , 0) +  *q* ( *i* , 1) +  *q* ( *i* , 2) = 1,  *q* ( *i* ,  *j* ) ≠ 0。

Output

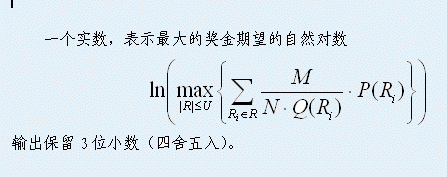
Samples

1 10 10 1
0.3 0.2 0.5 0.7 0.2 0.1

1.609