#P9901. 『PG2』弯曲半平面直线同向图最大流
『PG2』弯曲半平面直线同向图最大流
Description
若能将有向图 画在平面上,使得点在一条直线上,任意两条边(可以为弯曲的弧线)仅在重合顶点处相交,且边上的所有点都在直线同侧,且每条边的起点到终点的射线的方向相同,则称 是弯曲半平面直线同向图。对于一个弯曲半平面直线同向图给定 个点, 条有向边,给定每条边的容量,求从点 到点 的最大流。
Input Format
第一行包含四个正整数 、、、,用空格分隔,分别表示点的个数、有向边的个数、源点序号、汇点序号。
接下来 行每行包含三个正整数 、、,用空格分隔,表示第 条有向边从 出发,到达 ,容量为 。
Output Format
一个整数,表示 到 的最大流。
5 7 1 5
1 2 1
2 3 1
3 4 1
4 5 1
2 4 1
1 4 1
1 5 1
2
Hint
无重边自环。
对于 的数据 。
对于 的数据 。
对于 的数据 ,,,。
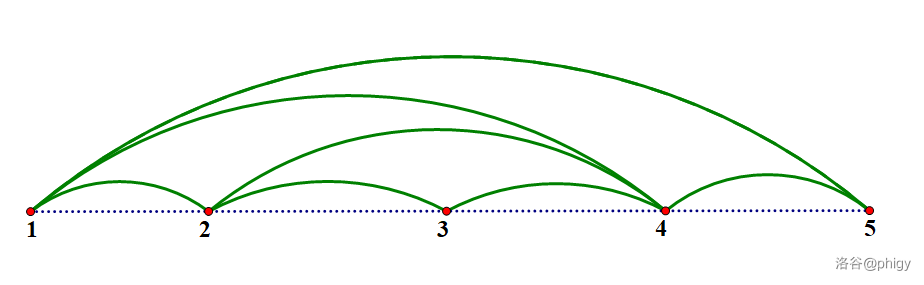
样例解释 1

 京公网安备 11011102002149号
京公网安备 11011102002149号