Description
给你一个 n 个顶点 m 条边的连通无向图,定义 u 与 v 的距离 d(u,v) 为从 u 到 v 最短路径上经过的边数。
现在请你求出 ∑u=1n∑v=u+1nd(u,v)。
第一行给定两个整数 n(1≤n≤105),m(n−1≤m≤n+42),分别表示点数和边数。
接下来 m 行,每行 2 个整数 xi 和 yi(1≤xi,yi≤n,xi=yi),表示 xi 和 yi 之间有一条边。
保证没有重边和自环。
输出 ∑u=1n∑v=u+1nd(u,v)。
4 4
1 2
2 3
3 1
3 4
8
7 10
1 2
2 6
5 3
5 4
5 7
3 6
1 7
5 1
7 4
4 1
34
Hint
对于所有数据保证 1≤n≤105,n−1≤m≤n+42,1≤xi,yi≤n 且 xi=yi。
样例一的图是:
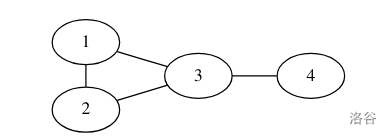
其中 d(1,2)=1,d(1,3)=1,d(1,4)=2,d(2,3)=1,d(2,3)=2,d(3,4)=1,总和为 1+1+2+1+2+1=8。
样例二为:
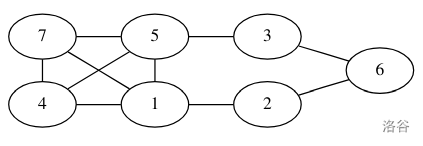



 京公网安备 11011102002149号
京公网安备 11011102002149号