#P9689. Bina.
Bina.
Description
小 J 家门前有两棵树,一棵是二叉树,一棵是三叉树。
你被小 J 叫来修剪他的二叉树,使得他的二叉树的“美丽值”最大,所谓一棵树的美丽值 这棵树的点的编号之和 这棵树的深度(结果向下取整)。
这棵二叉树有一个构建参数 ,构建方式如下:
void build(int s,int t,int p){
if(s==t) return ;
build(s,(s+t)/2,2*p);
build((s+t)/2+1,t,2*p+1);
add_edge(p,2*p),add_edge(p,2*p+1);
}
int main(){
build(1,n,1);
return 0;
}
其中 build(s,t,p) 函数参数中的 是当前点的编号,add_edge(x,y) 函数是指将编号为 的点向编号为 的点连接一条有向边。
容易发现这棵树的根节点是 ,并且我们规定节点的深度为节点到根节点路径上经过的点的个数(包括自己和根节点),这棵树的深度即为所有节点深度的最大值。
对于 的情况,最后构建出来的结果如下,这棵树的深度为 ,你需要选择一个深度 把深度大于 的点都剪掉,但是 必须大于等于 且小于等于这棵树的深度。
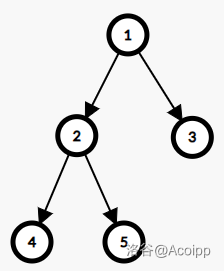
小 J 还给了你一个要求,你剪去的节点个数一定得大于等于 他才会高兴,你需要保证让他高兴的同时树的“美丽值”最大。
现在小 J 给了你构建树的参数 和至少剪的节点个数 ,要你求出来他的树在你修剪后最大的美丽值是多少,如果无论如何你也不可能让小 J 高兴,输出 。
Input Format
本题有多组数据。
第一行一个正整数 ,表示数据组数。
对于每组数据:
输入共一行两个整数 ,表示构建二叉树的参数和你至少剪掉的节点个数。
Output Format
对于每组数据:输出一行一个整数,表示能够获得的最大的“美丽值”,如果无法让小 J 高兴,输出 。
6
3 0
3 1
3 2
3 3
3 4
3 5
5
3
3
1
1
-1
10
5 5
10 0
999 155
135 92
1000232 234255
10293845 1239485
123948 1239454
12394 2131094
1000000000 98765432
1000000000 999999999
3
40
52377
1161
27487764480
5864061665280
-1
-1
19215358392218419
4969489234738635
Hint
【样例解释 #1】
对于第一组样例, 都等于 ,构建出来的树同题面所示。
如果我们选择把深度大于 的节点全部剪掉,那么我们剪掉了 共 个节点,美丽值为 。
如果我们选择把深度大于 的节点全部剪掉,那么我们剪掉了 共 个节点,美丽值为 。
如果我们选择把深度大于 的节点全部剪掉,那么我们没有剪掉任何节点,美丽值为 。
所以对于 的情况,答案为 ;对于 的情况,答案为 ;对于 的情况,答案为 ;其它情况,无解输出 。
【数据范围】
对于所有测试数据,满足 ,,。
本题开启捆绑测试,所有数据范围均相同的测试点捆绑为一个 。
各测试点的附加限制如下表所示。
| 测试点 | 特殊限制 | |||
|---|---|---|---|---|
| 无 | ||||
| 无 | ||||
| 所有 均相同 | ||||
| 无 |

 京公网安备 11011102002149号
京公网安备 11011102002149号