题目背景

这是一道交互题，你只需要实现代码中要求的函数。

你的代码不需要引用任何额外的头文件，也不需要实现 main 函数。

本题仅支持 C++ 语言提交。但请勿使用 C++14 (GCC 9)

题目描述

从布达佩斯机场到 Forrás 酒店有一条单向单车道的公路，公路的长度为 $L$ 公里。

IOI 2023 活动期间，有 $N+1$ 辆巴士在这条公路上行驶。巴士从 $0$ 到 $N$ 依次编号。巴士 $i$（$0 \le i \lt N$）计划在活动的第 $T[i]$ 秒从机场出发，行驶一公里用时 $W[i]$ 秒。巴士 $N$ 是备用巴士，行驶一公里用时 $X$ 秒。它从机场出发的时间 $Y$ 尚未确定。

巴士在这条公路上行驶时一般不允许超车，但允许在一些被称为调度站的地方进行超车。公路上一共有 $M$ 个调度站（$M \gt 1$），从 $0$ 到 $M - 1$ 依次编号，位于公路的不同位置。调度站 $j$（$0 \le j \lt M$）的位置在机场出发后沿公路的 $S[j]$ 公里处。调度站按照从机场开始的距离递增排列，也就是对于每个 $0 \le j \le M - 2$，有 $S[j] \lt S[j+1]$。首个调度站设在机场，最后一个设在酒店。也就是说，$S[0] = 0$，$S[M-1] = L$。

每辆巴士都以指定的最快速度行驶，除非它遇到前面有比它慢的巴士。在这种情况下，后面的快车会被前面的慢车压着，被迫以慢车的速度行驶。这种情况会持续到两车到达下一个调度站。在那里，快车会完成对慢车的超越。

形式化地说，对于满足 $0 \le i \le N$ 且 $0 \le j \lt M$ 的每组 $i$ 和 $j$，巴士 $i$ 到达调度站 $j$ 的时间 $t_{i,j}$（以秒为单位）定义如下：对于每个 $0 \le i \lt N$，有 $t_{i,0} = T[i]$。另有 $t_{N,0} = Y$。对于满足 $0 \lt j \lt M$ 的每个 $j$：

• 定义巴士 $i$ 到达调度站 $j$ 的期望到达时间 $e_{i,j}$（以秒为单位）为巴士 $i$ 到达调度站 $j-1$ 之后以全速行驶到达调度站 $j$ 的时间。也就是说，
  • 对于每个 $0 \le i \lt N$，有 $e_{i,j} = t_{i,j-1} + W[i] \cdot (S[j]-S[j-1])$；
  • 另有 $e_{N,j} = t_{N,j-1} + X \cdot (S[j]-S[j-1])$。
• 巴士 $i$ 到达调度站 $j$ 的时间，是巴士 $i$ 到达调度站 $j$ 的期望到达时间，以及其他比巴士 $i$ 早到调度站 $j-1$ 的巴士到达调度站 $j$ 的期望到达时间中的最大值。形式化地说，$t_{i,j}$ 是 $e_{i,j}$ 和所有满足 $0 \le k \le N$ 且 $t_{k,j-1} \lt t_{i,j-1}$ 的 $e_{k,j}$ 中的最大值。

IOI 组委会想要调度备用巴士（巴士 $N$）。你的任务是回答组委会的 $Q$ 个问题，问题的形式如下：给定备用巴士从机场出发的时间 $Y$（以秒为单位），它将于何时到达酒店？

输入格式

评测程序示例按以下格式读取输入：

• 第 $1$ 行：$L \; N \; X \; M \; Q$
• 第 $2$ 行：$T[0] \; T[1] \; \ldots \; T[N-1]$
• 第 $3$ 行：$W[0] \; W[1] \; \ldots \; W[N-1]$
• 第 $4$ 行：$S[0] \; S[1] \; \ldots \; S[M-1]$
• 第 $5 + k$ 行（$0 \le k \lt Q$）：问题 $k$ 的 $Y$

输出格式

评测程序示例按以下格式打印你的答案：

• 第 $1 + k$ 行（$0 \le k \lt Q$）：问题 $k$ 中 arrival_time 的返回值

6 4 10 4 2
20 10 40 0
5 20 20 30
0 1 3 6
0
50

60
130

提示

【实现细节】

你的任务是实现以下函数：

void init(int L, int N, int64[] T, int[] W, int X, int M, int[] S)

• $L$：公路的长度
• $N$：常规（非备用）巴士的数量
• $T$：长度为 $N$ 的数组，描述常规巴士计划从机场出发的时间。
• $W$：长度为 $N$ 的数组，描述常规巴士的最大速度。
• $X$：备用巴士行驶一公里所需的时间
• $M$：调度站的数量
• $S$：长度为 $M$ 的数组，描述从机场到调度站的距离。
• 对于每个测试用例，这个函数都恰好调用一次，发生在对任何 arrival_time 的调用之前。

int64 arrival_time(int64 Y)

• $Y$：备用巴士（巴士 $N$）计划从机场出发的时间
• 这个函数应该返回备用巴士到达酒店的时间。
• 这个函数恰好调用 $Q$ 次。

---

【例子】

考虑以下调用序列：

init(6, 4, [20, 10, 40, 0], [5, 20, 20, 30], 10, 4, [0, 1, 3, 6])

忽略巴士 $4$（它还没有确定出发时间），下表列出了巴士到达每个调度站的期望时间和实际时间：

$i$		$t_{i,0}$		$e_{i,1}$	$t_{i,1}$		$e_{i,2}$	$t_{i,2}$		$e_{i,3}$	$t_{i,3}$
$0$		$20$		$25$	$30$		$40$			$55$
$1$		$10$		$30$			$70$			$130$
$2$		$40$		$60$			$100$			$160$	$180$
$3$		$0$		$30$			$90$			$180$

巴士到达调度站 $0$ 的时间就是它计划从机场出发的时间。也就是说，对于 $0 \le i \le 3$，$t_{i,0} = T[i]$。

到达调度站 $1$ 的期望时间和实际时间计算如下：

• 调度站 $1$ 的期望到达时间：
  • 巴士 $0$：$e_{0,1} = t_{0,0} + W[0] \cdot (S[1]-S[0]) = 20 + 5 \cdot 1 = 25$。
  • 巴士 $1$：$e_{1,1} = t_{1,0} + W[1] \cdot (S[1]-S[0]) = 10 + 20 \cdot 1 = 30$。
  • 巴士 $2$：$e_{2,1} = t_{2,0} + W[2] \cdot (S[1]-S[0]) = 40 + 20 \cdot 1 = 60$。
  • 巴士 $3$：$e_{3,1} = t_{3,0} + W[3] \cdot (S[1]-S[0]) = 0 + 30 \cdot 1 = 30$。
• 调度站 $1$ 的到达时间：
  • 巴士 $1$ 和 $3$ 早于巴士 $0$ 到达调度站 $0$，所以 $t_{0,1} = \max([e_{0,1},e_{1,1},e_{3,1}]) = 30$。
  • 巴士 $3$ 早于巴士 $1$ 到达调度站 $0$，所以 $t_{1,1} = \max([e_{1,1},e_{3,1}]) = 30$。
  • 巴士 $0$、巴士 $1$ 和巴士 $3$ 早于巴士 $2$ 到达调度站 $0$，所以 $t_{2,1} = \max([e_{0,1},e_{1,1},e_{2,1},e_{3,1}]) = 60$。
  • 没有比巴士 $3$ 更早到达调度站 $0$ 的巴士，所以 $t_{3,1} = \max([e_{3,1}]) = 30$。

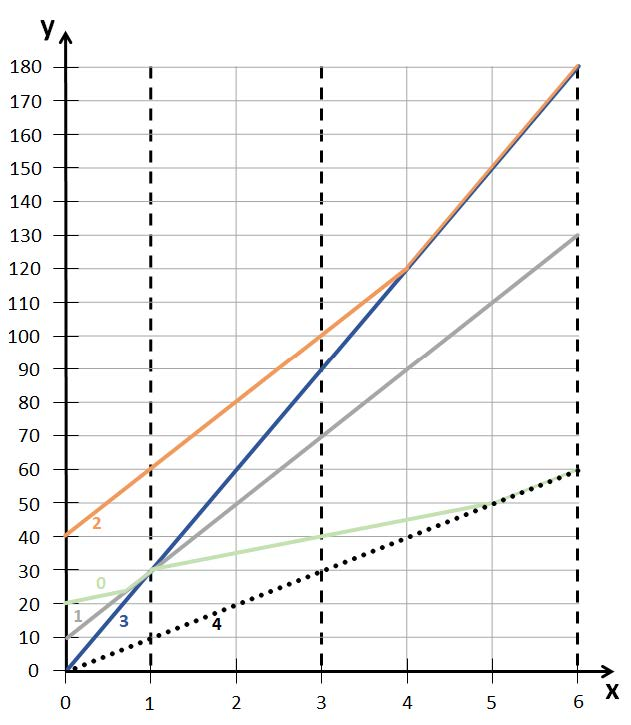
arrival_time(0)

巴士 $4$ 行驶一公里需要 $10$ 秒，现在计划在第 $0$ 秒从机场出发。 这种情况下，下表列出每辆巴士的到达时间。 常规巴士期望和实际到达时间的唯一变动用下划线标注。

$i$		$t_{i,0}$		$e_{i,1}$	$t_{i,1}$		$e_{i,2}$	$t_{i,2}$		$e_{i,3}$	$t_{i,3}$
$0$		$20$		$25$	$30$		$40$			$55$	$\underline{60}$
$1$		$10$		$30$			$70$			$130$
$2$		$40$		$60$			$100$			$160$	$180$
$3$		$0$		$30$			$90$			$180$
$4$				$10$			$30$			$60$

由此可知巴士 $4$ 在第 $60$ 秒到达酒店。 因此，函数应该返回 $60$。

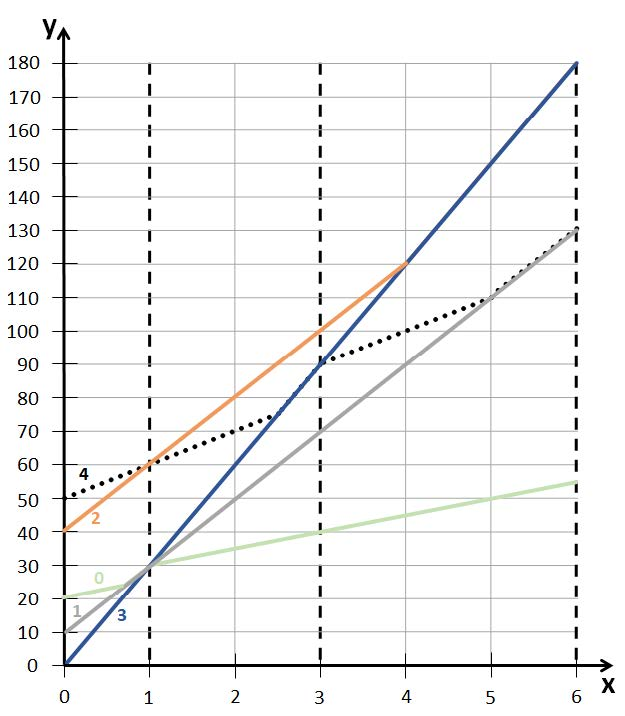
arrival_time(50)

巴士 $4$ 现在计划在第 $50$ 秒从机场出发。 这种情况下，与初始表格相比，常规巴士的到达时间没有变化。 下表列出了到达时间。

$i$		$t_{i,0}$		$e_{i,1}$	$t_{i,1}$		$e_{i,2}$	$t_{i,2}$		$e_{i,3}$	$t_{i,3}$
$0$		$20$		$25$	$30$		$40$			$55$
$1$		$10$		$30$			$70$			$130$
$2$		$40$		$60$			$100$			$160$	$180$
$3$		$0$		$30$			$90$	$90$		$180$
$4$		$50$		$60$			$80$			$120$	$130$

巴士 $4$ 和较慢的巴士 $2$ 同时到达调度站 $1$，然后巴士 $4$ 超过了巴士 $2$。 接着，巴士 $4$ 在调度站 $1$ 和 $2$ 之间行驶时被巴士 $3$ 压着，导致它到达调度站 $2$ 的时间是第 $90$ 秒，而不是第 $80$ 秒。 在过了调度站 $2$ 之后，巴士 $4$ 被巴士 $1$ 压着，直到它们到达酒店。 巴士 $4$ 在第 $130$ 秒到达酒店。 因此，函数应该返回 $130$。

将每辆巴士从机场出发到不同距离的时间画成折线图。 图中 x 轴表示从机场出发的距离（以公里为单位），y 轴表示时间（以秒为单位）。 竖的虚线标注了调度站的位置。 不同颜色的实线（标注了巴士的编号）表示四辆常规巴士。 黑色的点线表示备用巴士。

arrival_time(0)	arrival_time(50)

---

【约束条件】

• $1 \le L \le 10^9$
• $1 \le N \le 1\,000$
• $0 \le T[i] \le 10^{18}$（对于满足 $0 \le i \lt N$ 的每个 $i$）
• $1 \le W[i] \le 10^9$（对于满足 $0 \le i \lt N$ 的每个 $i$）
• $1 \le X \le 10^9$
• $2 \le M \le 1\,000$
• $0 = S[0] \lt S[1] \lt \cdots \lt S[M-1] = L$
• $1 \le Q \le 10^6$
• $0 \le Y \le 10^{18}$

---

【子任务】

1. （9 分）$N = 1, Q \le 1\,000$
2. （10 分）$M = 2, Q \le 1\,000$
3. （20 分）$N, M, Q \le 100$
4. （26 分）$Q \le 5\,000$
5. （35 分）没有额外的约束条件。