题目背景

这是一道交互题，你只需要实现代码中要求的函数。

你的代码不需要引用任何额外的头文件，也不需要实现 main 函数。

本题仅支持 C++ 语言提交。

题目描述

匈牙利有 $N$ 个城市，编号依次为 $0$ 到 $N - 1$。

这些城市之间由 $N - 1$ 条双向道路连接，编号为 $0$ 至 $N - 2$。对每个 $j$（$0 \le j \le N - 2$），第 $j$ 条道路连接城市 $U[j]$ 和城市 $V[j]$，其长度为 $W[j]$，表示这两个城市之间的交通时间为 $W[j]$ 个时间单位。每条道路连接两个不同的城市，且每两个城市之间最多由一条道路连接。

两个不同城市 $a$ 和 $b$ 之间的一条路径是一个由不同城市组成的序列 $p_0, p_1, \ldots, p_t$，满足以下条件：

• $p_0 = a$，
• $p_t = b$，
• 对每个 $i$（$0 \le i \lt t$），存在一条道路连接 $p_i$ 和 $p_{i + 1}$。

利用这些道路从任意一个城市到任意一个其他的城市都是有可能的。换言之，任意两个不同城市之间都存在路径。
可以证明两个不同城市之间的路径是唯一的。

一条路径 $p_0, p_1, \ldots, p_t$ 的长度是这条路径上连接相邻城市的 $t$ 条道路的长度之和。

在匈牙利，很多人都会在建国日去参加在两个主要城市举行的庆祝活动。当庆祝活动结束时，他们会回家。政府为了防止人群干扰当地人，所以决定在特定时刻封锁城市。每个城市被政府分配一个非负的封锁时刻。政府决定所有城市的封锁时刻总和不得超过 $K$。具体来说，对每个 $i$（$0 \leq i \leq N - 1$），分配给城市 $i$ 的封锁时刻是一个非负整数 $c[i]$。所有 $c[i]$ 之和不超过 $K$。

考虑一个城市 $a$ 和某个封锁时刻的分配方案，我们说城市 $b$ 是从城市 $a$ 可达的当且仅当以下两种情况中的任意一种情况成立。

情况 1：$b = a$。

情况 2：这两个城市之间的路径 $p_0, \ldots, p_t$ （$p_0 = a$ 且 $p_t = b$）满足以下条件：

• 路径 $p_0, p_1$ 的长度最多为 $c[p_1]$，并且
• 路径 $p_0, p_1, p_2$ 的长度最多为 $c[p_2]$，并且
• $\ldots$
• 路径 $p_0, p_1, p_2, \ldots, p_t$ 的长度最长为 $c[p_t]$。

今年，两个主要的庆祝地点位于城市 $X$ 和 $Y$。
对于每一个封锁时刻的分配方案，可以定义一个便利分数，其定义为下面两个数字之和：

• 从城市 $X$ 可达的城市个数。
• 从城市 $Y$ 可达的城市个数。

注意如果一个城市既能从城市 $X$ 可达也能从城市 $Y$ 可达，那么它在计算便利分数时计算两次。

你的任务是计算能被某个封锁时刻分配方案实现的最大便利分数。

输入格式

令 $C$ 表示场景数，即调用 max_score 的次数。 评测程序实例按以下格式读取输入：

• 第 $1$ 行：$C$

以下是 $C$ 个场景的描述。

评测程序实例按以下格式读取每个场景的描述：

• 第 $1$ 行：$N \; X \; Y \; K$
• 第 $2 + j$ 行（$0 \le j \le N - 2$）：$U[j] \; V[j] \; W[j]$

输出格式

评测程序实例按以下格式为每个场景打印单独一行

• 第 $1$ 行： max_score 的返回值

2
7 0 2 10
0 1 2
0 3 3
1 2 4
2 4 2
2 5 5
5 6 3
4 0 3 20
0 1 18
1 2 1
2 3 19

6
3

提示

【实现细节】

你要实现以下函数。

int max_score(int N, int X, int Y, int64 K, int[] U, int[] V, int[] W)

• $N$：城市的个数
• $X$，$Y$：两个主要庆祝城市
• $K$：封锁时刻总和的上界
• $U$，$V$： 长度为 $N - 1$ 的描述道路连接情况的数组
• $W$：长度为 $N - 1$ 的描述道路长度的数组
• 该函数要返回能被某个封锁时刻分配方案实现的最大便利分数
• 每个测试用例可以多次调用该函数

【例子】

考虑以下调用：

max_score(7, 0, 2, 10,
          [0, 0, 1, 2, 2, 5], [1, 3, 2, 4, 5, 6], [2, 3, 4, 2, 5, 3])

这对应以下道路网络：

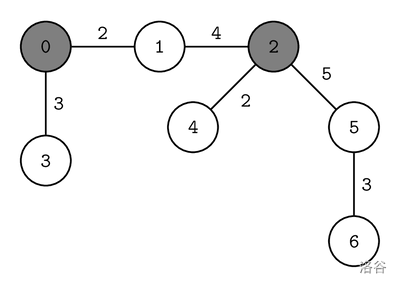
假设封锁时刻如下分配：

城市	$0$	$1$	$2$	$3$	$4$	$5$	$6$
封锁时刻	$0$	$4$	$0$	$3$	$2$	$0$

注意所有封锁时刻之和为 $9$，不超过 $K = 10$。城市 $0$，$1$ 和 $3$ 都是从城市 $X$（$X = 0$）可达的，而城市 $1$，$2$ 和 $4$ 都可以从城市 $Y$（$Y = 2$）可达。 因此，便利分数为 $3+3 = 6$。不存在封锁时刻分配方案使得便利分数大于 $6$，所以该函数应该返回 $6$。

考虑另外一个调用：

max_score(4, 0, 3, 20, [0, 1, 2], [1, 2, 3], [18, 1, 19])

这对应以下道路网络：

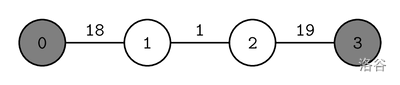
假设封锁时间如下分配：

城市	$0$	$1$	$2$	$3$
封锁时刻	$0$	$1$	$19$	$0$

城市 $0$ 从城市 $X$（$X = 0$）可达，而城市 $2$ 和 $3$ 都是可以从城市 $Y$（$Y=3$）可达的。因此，便利分数是 $1 + 2 = 3$。不存在封锁时刻分配方案使得便利分数大于 $3$，所以函数应该返回 $3$。

【约束条件】

• $2 \le N \le 200\,000$
• $0 \le X \lt Y \lt N$
• $0 \le K \le 10^{18}$
• $0 \le U[j] \lt V[j] \lt N$ (对每个 $j$ 满足 $0 \le j \le N - 2$)
• $1 \le W[j] \le 10^6$ (对每个 $j$ 满足 $0 \le j \le N - 2$)
• 利用这些道路可以从任意一个城市走到任意另外一个城市。
• $S_N \le 200\,000$，其中 $S_N$ 是所有调用函数 max_score 的 $N$ 的总和。

【子任务】

我们说一个道路网络是线性的如果道路 $i$ 连接城市 $i$ 和 $i+1$（对每个$0 \le i \le N - 2$ 的 $i$）。

1. （8 分）从城市 $X$ 到城市 $Y$ 的路径长度大于 $2K$。
2. （9 分）$S_N \le 50$，道路网络是线性的。
3. （12 分）$S_N \le 500$，道路网络是线性的。
4. （14 分）$S_N \le 3\,000$，道路网络是线性的。
5. （9 分）$S_N \le 20$
6. （11 分）$S_N \le 100$
7. （10 分）$S_N \le 500$
8. （10 分）$S_N \le 3\,000$
9. （17 分）无额外的约束条件。