题目描述

给定一棵树，节点有颜色，在树上距离为 $2$ 的点连边（仍保留原来的边），求新图中颜色相同且连通的非空点集数量。由于答案可能非常大，您只需输出答案对 $10^9+7$ 取模的值。

点集连通的定义：对于图 $G(V,E)$，$V$ 的一个子集 $V'$ 是连通点集，当且仅当 $G(V',E')$ 是一个连通图，其中边集 $E'=\{(u,v)|(u,v)\in E\land u \in V'\land v\in V'\}$。

输入格式

第一行一个正整数 $n$，表示节点个数。

接下来一行 $n$ 个正整数，第 $i$ 个正整数 $c_i$ 表示第 $i$ 个节点的颜色。

接下来 $n-1$ 行每行两个正整数 $u,v$ 表示原树有一条 $u$ 到 $v$ 的边。

输出格式

一行一个整数，表示答案对 $10^9+7$ 取模的值。

4
1 2 1 1
1 2
2 3
2 4

8

6
1 2 2 2 1 2
5 3
2 1
4 5
6 3
3 1

14

16
1 1 2 1 1 2 2 2 1 1 2 1 1 1 2 1
12 8
14 9
10 8
1 16
7 12
6 1
14 8
3 1
12 5
1 13
12 2
1 12
15 8
11 5
4 12

442

16
11 11 11 11 11 11 11 11 11 11 11 11 11 11 11 11
4 14
4 15
12 13
2 5
7 15
10 2
15 8
15 13
9 11
13 11
3 15
8 16
6 13
1 4
10 4

27454

9
3 3 2 3 2 4 2 3 3
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9

16

提示

样例 1 中，原树如下图所示：

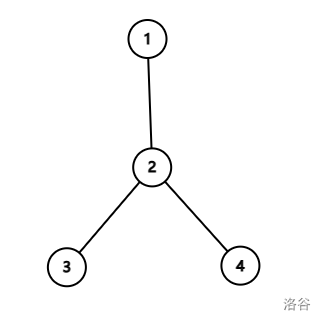
树上距离为 $2$ 的点连边后，新图如下图所示：

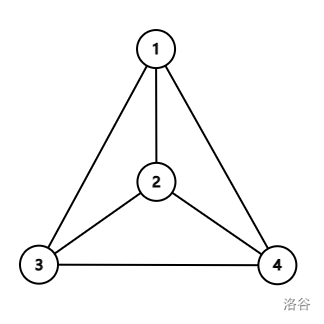
则 $8$ 个颜色相同且连通的非空点集分别是：$\{1\},\{2\},\{3\},\{4\},\{1,3\},\{1,4\},\{3,4\},\{1,3,4\}$。

本题开启捆绑测试。

• 特殊性质 A：所有节点的颜色不相同。
• 特殊性质 B：给出的树是菊花，具体地，第 $i$ 条边连接节点 $1$ 和节点 $i+1$。
• 特殊性质 C：给出的树是链，具体地，第 $i$ 条边连接节点 $i$ 和节点 $i+1$。
• 特殊性质 D：所有节点的颜色相同。

对于全部数据，满足 $2\leq n\leq 10^5$，$1\leq c_i\leq n$。