#P9542. [湖北省选模拟 2023] 棋圣 / alphago
[湖北省选模拟 2023] 棋圣 / alphago
Description
小 K 是一名棋手,厌倦了传统围棋之后,他发明了一种新式围棋。
新式围棋是一种单人游戏。这个游戏的棋盘是一张包含 个顶点, 条边的无向连通图,并且不存在重边和自环。同时,每条边有一个权值,第 条边的权值为 。
游戏开始时,每个顶点上可能有一颗黑棋或者一颗白棋,或者什么也没有。至少有一个顶点上没有棋子。 接下来,玩家需要进行若干次操作。每次的操作形式如下:
首先,选定一个上面没有棋子的顶点 。可以说明,在题目数据范围下,一定存在这样的顶点。
接下来,对于每一颗棋子,若它位于顶点 ,则玩家需任选一条从 到 的简单路径,并将这颗棋子沿着这条简单路径移动一步。形式化地,一条简单路径为一个顶点序列 ,满足 , , 互不相同,且 和 之间存在一条边。在操作之后,这颗棋子将被移动至顶点 。
需要注意的是,虽然在游戏开始时每个顶点上至多存在一颗棋子,但在若干次操作之后一个顶点上可能有多个棋子。对于同一个顶点上的不同棋子,一次操作中选取的简单路径可以不同。
玩家可以在进行任意次操作(可以是 次)之后进行点目,即结算游戏分数。对于每一对颜色不同的棋子,若它们所在的顶点之间由一条权值为 的边直接相连,则称它们围住了这条边,会使玩家得到 的目数。而一个玩家所得到的目数即所有棋子对产生的目数之和。
现小 K 给了你一张游戏开始时的棋盘,请你帮他求出在这张棋盘上最多可能得到的目数。
Input Format
输入共 行。
第一行三个整数 ,分别表示点和边的数量,以及棋子的数量。
接下来 行,每行两个整数 ,表示顶点 上有一颗颜色为 的棋子。其中 表示一颗黑棋, 表示一颗白棋。
接下来 行每行三个整数 ,表示图中有一条连接 和 的权值为 的边。
Output Format
输出一行一个整数,为所求答案。
3 2 2
1 0
2 1
1 2 1
2 3 2
2
4 4 3
1 1
2 1
3 0
1 2 1
2 3 1
3 4 1
4 1 3
3
见选手目录下的 alphago/alphago3.in 与 alphago/alphago3.ans。
见选手目录下的 alphago/alphago3.in 与 alphago/alphago3.ans。
见选手目录下的 alphago/alphago4.in 与 alphago/alphago4.ans。
见选手目录下的 alphago/alphago4.in 与 alphago/alphago4.ans。
见选手目录下的 alphago/alphago5.in 与 alphago/alphago5.ans。
见选手目录下的 alphago/alphago5.in 与 alphago/alphago5.ans。
Hint
样例 1 解释
对于第一组样例,可以选定顶点 ,然后将 号点上的黑棋移动到顶点 ,将 号点的黑棋移动到顶点 ,这样两颗棋子所在的顶点之间由一条边权为 的边连接,产生的目数为 。
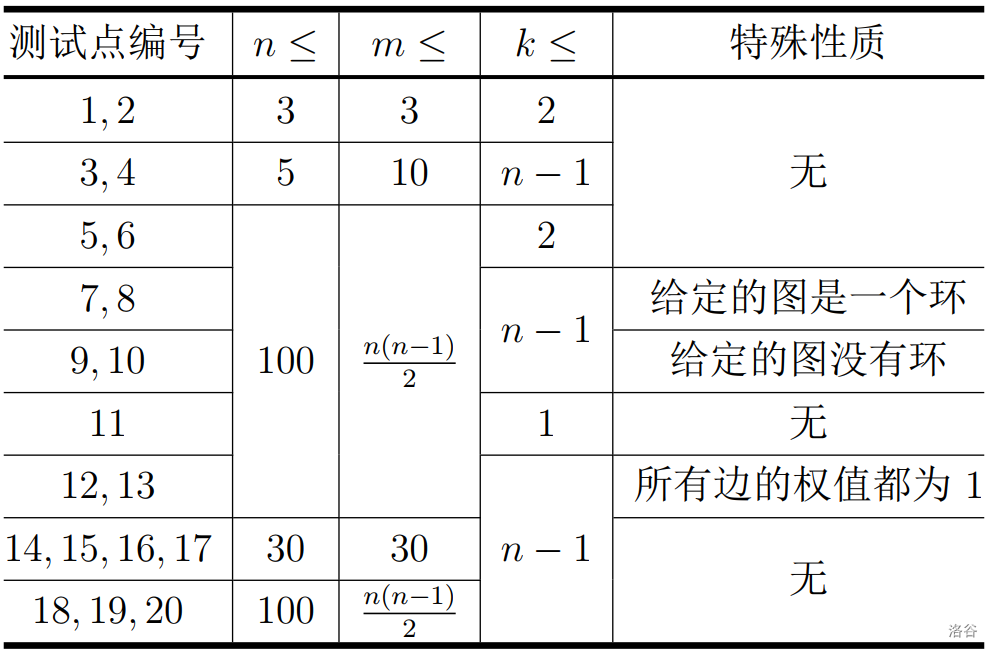
子任务
对于所有测试数据,保证 ,,,。

 京公网安备 11011102002149号
京公网安备 11011102002149号