题目背景

JOISC2022 D1T2

题目描述

京都是世界级的观光圣地，它也被称为网格城市。你来到了京都观光，并且你计划步行游览一个著名的景点。本题中，我们考虑如下的简化问题。

在城市中，有 $H$ 条东西方向的街道和 $W$ 条南北方向的街道，因此城市是一个 $(H-1)\times(W-1)$ 的网格。从北数第 $i$ 条街道和从西数第 $j$ 条街道的交叉点记作路口 $(i,j)$。

不同的街道可能有不同的材质、宽度和拥挤程度，因此你的步行速度有可能不同。对于每条街道，你的步行速度如下：

• 如果你在从北数第 $i$ 条街道上行走单位长度，需要 $A_i$ 秒。即从路口 $(i,c)~\left(i\in[1,H],c\in[1,W)\right)$ 走到路口 $(i,c+1)$ 需要 $A_i$ 秒。

• 如果你在从西数第 $j$ 条街道上行走单位长度，需要 $B_j$ 秒。即从路口 $(c,j)~\left(c\in[1,H),j\in[1,W]\right)$ 走到路口 $(c+1,j)$ 需要 $B_j$ 秒。

你现在在路口 $(1,1)$，你想前往 $(H,W)$，你必须沿着街道行走，并且你不希望走远路，即你不会向北或向西走。

你希望尽早到达目的地，请你求出，在给定的条件下，从路口 $(1,1)$ 前往路口 $(H,W)$ 所需的最少时间。

输入格式

第一行两个整数 $H,W$ 表示街道条数。

第二行 $H$ 个整数，第 $i$ 个整数 $A_i$ 表示从北数第 $i$ 条东西方向街道的步行速度。

第三行 $W$ 个整数，第 $i$ 个整数 $B_i$ 表示从西数第 $i$ 条南北方向街道的步行速度。

输出格式

一行一个整数，表示所需的最小步行时间。

2 2
1 3
2 5

5

5 5
7 1 5 2 8
7 2 4 1 6

20

4 6
454863204 543362989 866044086 813602010
71574269 17945210 688720933 392135202 38174709 168241720

2737473954

提示

【样例解释 #1】

有两条从 $(1,1)$ 到 $(2,2)$ 的路线：

1. $(1,1)\rightarrow(1,2)\rightarrow(2,2)$，所需时间为 $1+5=6$ 秒。
2. $(1,1)\rightarrow(2,1)\rightarrow(2,2)$，所需时间为 $2+3=5$ 秒。

因此最少花费时间为 $5$ 秒。

这个样例满足所有子任务的限制。

【样例解释 #2】

最优路线如下图：

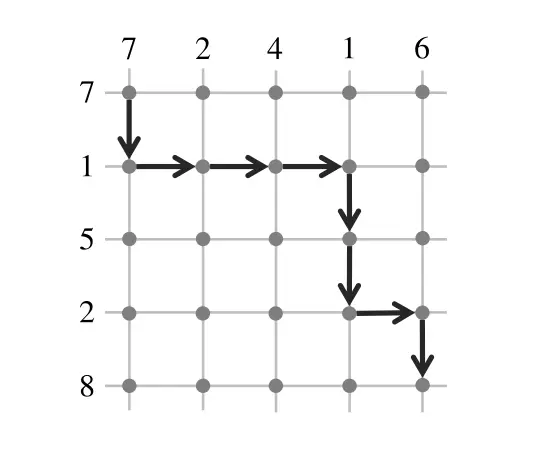
这个样例满足所有子任务的限制。

【样例解释 #3】

这个样例满足子任务 $1,3$ 的限制。

【数据范围】

对于所有数据，满足：

• $2\leq H,W\leq 100000$。
• $1\leq A_i\leq 10^9$ $(i\in[1,H])$。
• $1\leq B_i\leq 10^9$ $(i\in[1,W])$。

详细子任务附加限制及分值如下表所示：

子任务编号	附加限制	分值
$1$	$H,W\leq 1000$	$10$
$2$	$A_i\leq 1000, B_i\leq 1000$	$30$
$3$	无附加限制	$60$