#P9476. [_-0 B] 地铁
[_-0 B] 地铁
Description
A 市共有 个居民点,第 个居民点的人口为 ,同时有 条双向道路,构成一棵树,第 条双向道路连接居民点 和 ,人步行走过这条道路需要 的时间。
现 A 市政府决定开通一条地铁线路。地铁线路是树上的一条简单路径,若路径经过第 条道路,那么地铁从这条道路下方经过只需要 的时间,同时,地铁的进出站共需要花费 的时间。
已知,若一个人从一个居民点前往另一个居民点,如果这条路径与地铁经过的路径有至少一条公共边,那么就一定会选择尽可能多地乘坐地铁。如果没有公共边,那么就会选择完全步行。题目保证对于第 条道路有 。 我们认为,如果两个居民点的人口的乘积越大,那么有人想要在它们之间流动的可能性也越大。
现在,小 想知道在所有 种建造地铁线路的方案中,$\sum_{a=1}^{n-1}\sum_{b=a+1}^{n}(s_a \cdot s_b \cdot d_{a,b})$ 的最小值,其中 表示从居民点 前往 (或者从 前往 ,两者是相等的)所需要的时间。
但是他不会,所以他来求助万能的你。
Input Format
第一行,三个用空格分隔的整数 ,表示子任务编号,居民点个数和进出站所需要花费的时间。
接下来 行,每行一个整数 ,表示每个居民点的人口。
接下来 行,每行四个用空格分隔的整数 ,表示每条道路的两个端点,步行所需时间和地铁所需时间。
Output Format
一行,一个整数,表示所求的最小值。
答案可能超过 位整形表示范围,您可以使用 __int128 类型,其表示范围为 。
以下为 __int128 类型的输出模板:
#include <bits/stdc++.h>
using namespace std;
__int128 ans;
int main() {
/* Your code here */
string str;
if (!ans) {
str = "0";
} else {
str = "";
while (ans) {
str = ((char)(48 + ans % 10)) + str;
ans /= 10;
}
}
cout << str << endl;
return 0;
}
0 5 0
9
9
3
2
3
1 2 7 6
1 3 8 5
1 4 6 5
2 5 9 9
2262
0 10 86
50
6
84
50
83
67
93
55
93
70
1 2 94 7
1 3 97 4
1 10 98 12
2 4 89 1
2 7 98 1
4 5 99 13
4 6 96 5
5 8 95 5
5 9 97 7
33600416
Hint
样例 解释:
修建地铁前如下图所示:
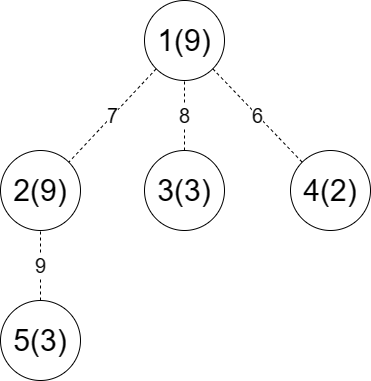
一种最优的修建地铁的方案为从 到 修建地铁。如下图所示(实线表示修建了地铁):
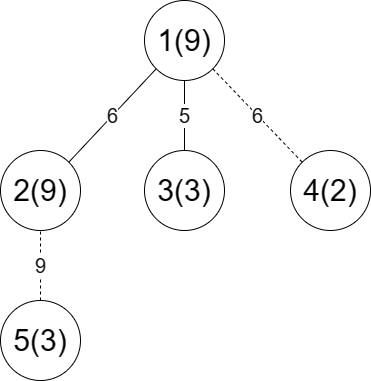
从 到 经过地铁,所需时间为:,对答案的贡献为:。
从 到 经过地铁,所需时间为:,对答案的贡献为:。
从 到 不经过地铁,所需时间为:,对答案的贡献为:。
从 到 经过地铁,所需时间为:,对答案的贡献为:。
从 到 经过地铁,所需时间为:,对答案的贡献为:。
从 到 经过地铁,所需时间为:,对答案的贡献为:。
从 到 不经过地铁,所需时间为:,对答案的贡献为:。
从 到 经过地铁,所需时间为:,对答案的贡献为:。
从 到 经过地铁,所需时间为:,对答案的贡献为:。
从 到 经过地铁,所需时间为:,对答案的贡献为:。
综上,答案为:。
可以证明不存在更优的修建地铁的方案。
本题采用捆绑测试且使用子任务依赖。
| 编号 | 分值 | 性质 | 依赖 | |
|---|---|---|---|---|
| N/A | 样例 | 无 | ||
| 无 | ||||
| A | 无 | |||
| B | ||||
| C | ||||
| D | ||||
| 无 | ||||
特殊性质 A:
特殊性质 B:
特殊性质 C:每一个点的度数都不超过
特殊性质 D:

 京公网安备 11011102002149号
京公网安备 11011102002149号