#P9323. [EGOI 2022] Toy Design / 玩具设计
[EGOI 2022] Toy Design / 玩具设计
Description
本题是一道 Grader 交互题。
你在一个设计玩具的公司工作。一个将被制作的玩具如下:有 个大头针,编号从 到 ,从盒子中伸出。几对大头针被铁丝在盒子中相连。(换句话说,大头针和铁丝组成了一个无向图,其中大头针是节点、铁丝是边。)铁丝无法从盒子外部看到,唯一获得关于他们的信息的方法是对大头针使用一个检测器:我们选择两个大头针 (),检测器会告诉你这两个大头针是否连通,包括直接和间接。(因此,检测器告诉你图中这两个大头针之间是否有一条路径。)
我们称一组连接方式为玩具的设计方案。
你正在使用一个专用的软件来查询和进行设计。软件工作方式如下:从某个称为“ 号方案”的设计方案开始。他不会告诉你盒子内部的铁丝是什么样的。你需要重复进行以下的三步操作:
- 选择一个设计方案 和两个大头针 ()。
- 软件告诉你对这两个大头针使用检测器的结果。换句话说,它告诉你在设计方案 中 与 是否(直接或间接地)连通。
- 同时,如果这两个大头针在设计方案 中没有被直接或间接地连接,它会创建一个新的设计方案,包含设计方案 中的所有铁丝,同时添加一个直接连接 的铁丝。这个设计方案的编号为下一个可用的编号。(所以,第一个创建的设计方案是 号方案,然后是 号,以此类推。)请注意这不会修改设计方案 ,只会新建一个设计方案包含新的铁丝。
你的目标是使用这种操作获取尽可能多的 号方案的信息。
请注意并不总是可能求出 号方案的准确的铁丝连接方式,因为无法区分直接和间接的连接。例如,考虑如下的两种 的设计方案:
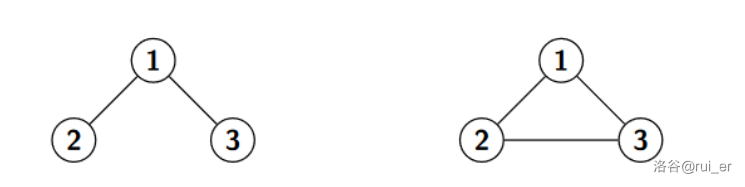
检测器会认为两种方案中任意一对大头针都连通,所以我们无法利用上述软件区分它们。
你的目标是求出任何一种设计方案,使得它与 号方案等价。两种设计方案等价当且仅当对于任意一对大头针,检测器在两种方案中都返回相同结果。
Output Format
交互方式
你需要实现一个函数:
void ToyDesign(int n, int max_ops);
作用是给出一种与 号方案等价的设计方案。你可以调用以下两个函数来实现这一点。你可以调用的第一个函数为:
int Connected(int a, int i, int j);
其中 ,,,且 不能超过目前已有的设计方案数。如果在设计方案 中,大头针 是(直接或间接地)连通的,它的返回值是 。否则,它的返回值是已有的设计方案数加一,就是包含 的所有铁丝以及一根连接 的铁丝的新的设计方案的编号。函数 Connected 可以被调用最多 max_ops 次。
当你的程序完成了需要的 Connected 调用,它应该描述一种等价于 号方案的设计方案。为了描述一个方案,程序应当调用:
void DescribeDesign(std::vector<std::pair<int, int>> result);
参数 result 是整数对的向量,描述大头针之间的直接铁丝连接。每对数描述一根铁丝,包含被连接的两个大头针的编号。在任意一对(无序的)大头针对之间必须只有至多一根铁丝,且不能有铁丝连接一个大头针和它自己。一旦调用这个函数,你的程序将被终止。
Hint
样例交互过程
| 选手程序 | Grader | 解释 |
|---|---|---|
ToyDesign(4, 20) |
玩具中有 个大头针。你需要在 次 Connected 调用内,给出任何一种等价于 号方案的设计方案。 |
|
Connected(0, 1, 2) |
返回 。 | 大头针 在 号方案中不直接或间接地连通。新的设计方案是 号。 |
Connected(1, 3, 2) |
返回 。 | 大头针 在 号方案中不直接或间接地连通。新的设计方案是 号。 |
Connected(0, 3, 4) |
返回 。 | 大头针 在 号方案中直接或间接地连通。没有新的设计方案。 |
DescribeDesign({{3, 4}}) |
描述一个只有一根铁丝的设计方案:连接大头针 。 |
数据范围
对于全部数据,。
- 子任务一( 分):,
max_ops为 。 - 子任务二( 分):,
max_ops为 。 - 子任务三( 分):,
max_ops为 。 - 子任务四( 分):,
max_ops为 。

 京公网安备 11011102002149号
京公网安备 11011102002149号