#P9085. [PA 2018] Wielokąty
[PA 2018] Wielokąty
Description
题目译自 PA 2018 Runda 5 Wielokąty 。
请求出满足以下条件的多边形的个数:
- 记该多边形的第 个顶点为 ,则 且 , 。
- 该多边形的任意一条边(不包含端点)不能经过格点(即横纵坐标都为整数的点)。
- 该多边形的每一条边的长度都是不超过 的整数。
- 该多边形是一个凸多边形,而且不能退化(不能出现三点共线,自切,不小于 的角)。
- 该多边形的每一条边都是线段。
由于满足条件的多边形数量太大,你只需要输出其对 取模后的值即可。
下图展示了三个不合法的多边形。第一个多边形的边经过了格点,第二个多边形退化了,第三个多边形不是凸的。而且第一,三个有的边长不是整数。
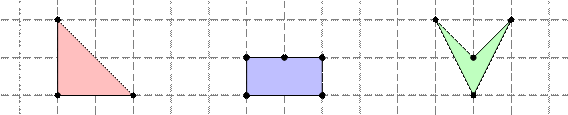
我们将两个多边形看做不相同的多边形,当且仅当它们有至少一个顶点不相同。
Input Format
输入只有一行,包含三个正整数 。
Output Format
输出一行一个整数,即为满足条件的多边形的数量对 取模后的值。
6 5 5
42
Hint
样例 1 解释
下图展示了 个合法多边形中的一个多边形。
可以验证,该多边形满足每一个条件。

数据范围
本题采用捆绑测试
对于 的数据,保证 。

 京公网安备 11011102002149号
京公网安备 11011102002149号