题目描述

X 星球的居民点很多。Pear 决定修建一个浩大的水利工程，以解决他管辖的 $N$ 个居民点的供水问题。现在一共有 $N$ 个水塔，同时也有 $N$ 个居民点，居民点在北侧从 $1$ 号到 $N$ 号自西向东排成一排；水塔在南侧也从 $1$ 号到 $N$ 号自西向东排成一排。

$N$ 条单向输水线（有水泵动力），将水从南侧的水塔引到北侧对应的居民点。

我们不妨将居民点和水塔都看做平面上的点，居民点坐标为 $(1,K) \sim (N,K)$，水塔为 $(1,0) \sim (N,0)$。

除了 $N$ 条纵向输水线以外，还有 $M$ 条单向的横向输水线，连接 $(X_i,Y_i)$ 和 $((X_i)+1,Y_i)$ 或者 $(X_i,Y_i)$ 和 $((X_i)-1,Y_i)$。前者被称为向右的水路，而后者是向左的。不会有两条水路重叠，即便它们方向不同。

布局的示意图如所示。

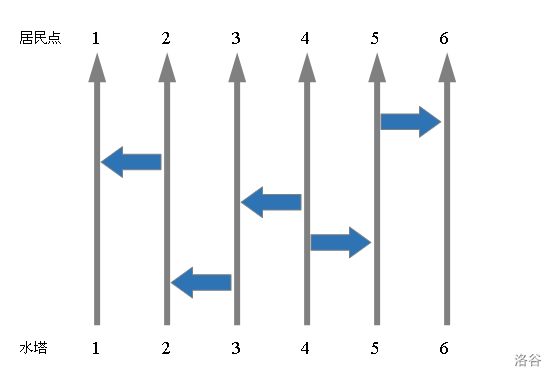
显然，每个水塔的水都可以到达若干个居民点（而不仅仅是对应的那个）。例如上图中，$4$ 号水塔可以到达 $3$ 、 $4$ 、 $5$ 、 $6$ 四个居民点。

现在 Pear 决定在此基础上，再修建一条横向单向输水线。为了方便考虑，Pear 认为这条水路应当是自左向右的，也就是连接了一个点和它右侧的点（例如上图中连接 $5$ 和 $6$ 两个纵线的横向水路）。

Pear 的目标是，修建了这条水路之后，能有尽可能多对水塔和居民点之间能到达。换句话说，设修建之后第 $i$ 个水塔能到达 $A_i$ 个点，你要最大化 $A_1+A_2+ \cdots +A_n$。

根据定义，这条路必须和 X 轴平行，但 Y 坐标不一定要是整数。注意：虽然输入中没有重叠的水路，但是你的方案可以将新修的输水线路与已有的水路重叠。

输入格式

输入第一行包含三个正整数 $N$，$M$，$K$，含义如题面所述：$N$ 是纵向线数，$M$ 横向线数，$K$ 是居民点纵坐标。

接下来 $M$ 行，每行三个整数。前两个正整数 $X_i,Y_i$ 表示水路的起点坐标；

$1 \le X_i \le N,0<Y_i<K$。

接下来一个数 $0$ 或者 $1$，如果是 $0$ 表示这条水路向左，否则向右。

保证水路都是合法的，也就是不会流向没有定义的地方。

输出格式

输出一行。是一个正整数，即：题目中要求的最大化的 $A_1+A_2+ \cdots +A_n$。

4 3 2
1 1 1
3 1 0
3 1 1

11

7 9 4
2 3 0
7 2 0
6 3 1
6 1 0
2 1 1
3 3 1
5 2 0
2 2 1
7 1 0

21

提示

对于 $20\%$ 的数据，$N,K \le 20$，$M \le 100$。

对于 $40\%$ 的数据，$N,K \le 100$，$M \le 1000$。

对于 $60\%$ 的数据，$N,K \le 1000$，$M \le 100000$。

对于 $100\%$ 的数据，$N,K \le 50000$，$M \le 10^5$。

时限 4 秒, 256M。蓝桥杯 2014 年第五届国赛