题目描述

栋栋每天骑自行车回家需要经过一条狭长的林荫道。道路由于年久失修，变得非常不平整。虽然栋栋每次都很颠簸，但他仍把骑车经过林荫道当成一种乐趣。

由于颠簸，栋栋骑车回家的路径是一条上下起伏的曲线，栋栋想知道，他回家的这条曲线的长度究竟是多长呢？更准确的，栋栋想知道从林荫道的起点到林荫道的终点，他的车前轮的轴（圆心）经过的路径的长度。

栋栋对路面进行了测量。他把道路简化成一条条长短不等的直线段，这些直线段首尾相连，且位于同一平面内。并在该平面内建立了一个直角坐标系，把所有线段的端点坐标都计算好。

假设栋栋的自行车在行进的过程中前轮一直是贴着路面前进的。

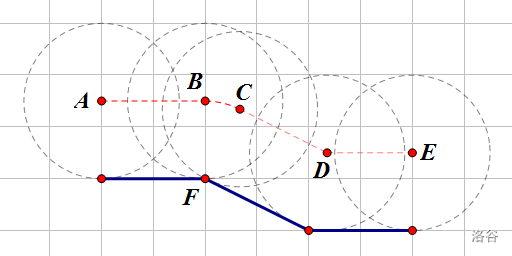
图 $1$ 给出了一个简单的路面的例子，其中蓝色实线为路面，红色虚线为车轮轴经过的路径。在这个例子中，栋栋的前轮轴从 $A$ 点出发，水平走到 $B$ 点，然后绕着地面的 $F$ 点到 $C$ 点（绕出一个圆弧），再沿直线下坡到 $D$ 点，最后水平走到 $E$ 点，在这个图中地面的坐标依次为：$(0,0),(2,0),(4,-1),(6,-1)$，前轮半径为 $1.50$，前轮轴前进的距离依次为：

$AB=2.0000$；弧长 $BC=0.6955$；$CD=1.8820$；$DE=1.6459$。

总长度为 $6.2233$。

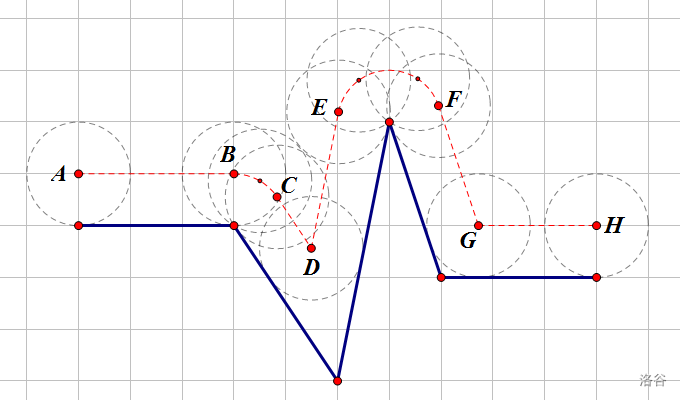
图 $2$ 给出了一个较为复杂的路面的例子，在这个例子中，车轮在第一个下坡还没下完时（$D$ 点）就开始上坡了，之后在坡的顶点要从 $E$ 绕一个较大的圆弧到 $F$ 点。这个图中前轮的半径为 $1$，每一段的长度依次为：

$AB=3.0000$；弧长 $BC=0.9828$；$CD=1.1913$；$DE=2.6848$；弧长 $EF=2.6224$；$FG=2.4415$；$GH=2.2792$。

总长度为 $15.2021$。

现在给出了车轮的半径和路面的描述，请求出车轮轴轨迹的总长度。

输入格式

输入的第一行包含一个整数 $n$ 和一个实数 $r$，用一个空格分隔，表示描述路面的坐标点数和车轮的半径。

接下来 $n$ 行，每个包含两个实数，其中第 $i$ 行的两个实数 $x_i,y_i$ 表示描述路面的第 $i$ 个点的坐标。

路面定义为所有路面坐标点顺次连接起来的折线。给定的路面的一定满足以下性质：

• 第一个坐标点一定是 $(0,0)$；
• 第一个点和第二个点的纵坐标相同；
• 倒数第一个点和倒数第二个点的纵坐标相同；
• 第一个点和第二个点的距离不少于车轮半径；
• 倒数第一个点和倒数第二个点的的距离不少于车轮半径；
• 后一个坐标点的横坐标大于前一个坐标点的横坐标，即对于所有的 $i$，$x_{i+1}>x_i$。

输出格式

输出一个实数，四舍五入保留两个小数，表示车轮轴经过的总长度。

你的结果必须和参考答案一模一样才能得分。数据保证答案精确值的小数点后第三位不是 $4$ 或 $5$。

4 1.50
0.00 0.00
2.00 0.00
4.00 -1.00
6.00 -1.00

6.22

6 1.00
0.00 0.00
3.00 0.00
5.00 -3.00
6.00 2.00
7.00 -1.00
10.00 -1.00

15.20

提示

对于 $20\%$ 的数据，$n=4$；

对于 $40\%$ 的数据，$n \le 10$；

对于 $100\%$ 的数据，$4 \le n \le 100$，$0.5 \le r \le 20.0$，$x_i \le 2000.0$，$-2000.0 \le y_i \le 2000.0$。

时限 1 秒, 64M。蓝桥杯 2013 年第四届国赛