#P8562. 十二重骗分法(Cheating XII)
十二重骗分法(Cheating XII)
Description
一阵恍惚过后,你发现自己坐在机房里。一看时间,现在竟然是 2202 年!你又环视了一下周围的情况,原来自己在 CSP-J 2202 的考场上。
你还没搞清楚情况时,似乎听见有人对你低语:「想知道怎么回事吗?那就展现你以往的能力,把这次的 CSP-J 也 AK 掉吧。」
于是你看到四个题分别是:
-
输入一个正整数 ,求 。
-
给定一个左右各有 个点的二分图,与其中的边,求它完美匹配的方案数,答案对 取模。
-
生命游戏(Conway's Game of Life)进行于一个无限大的二维网格上,每个格子要么是空地,要么有一个细胞。每个时刻都会进行一轮迭代,规则如下:
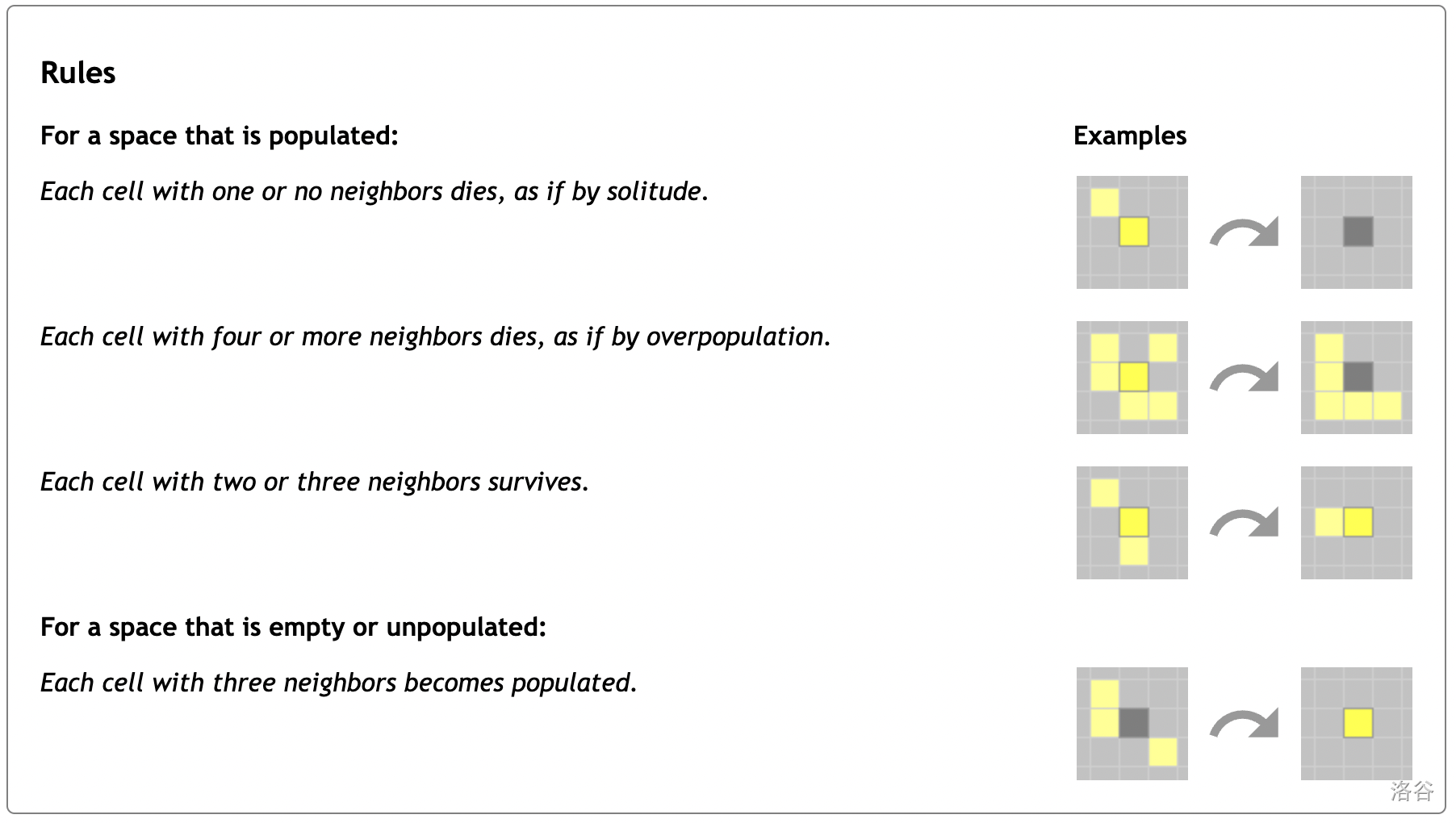
现在,给定你初始状态,求迭代 次后的细胞数。
ps:你可以在 这里 试玩。 -
给你一个 个点、 条边的无向图,每个点都可以涂上 种颜色中的一种,且相邻的点(即有边直接相连的点)不能有相同的颜色。求有多少种染色方案,答案对 取模。
「这怎么可能啊!」你差点惊叫出来。不过你发现,唯独你的电脑上有题目的输入数据!你想暴力跑出答案,却发现 2202 年的评测机性能和一百多年前没差别。
那该怎么办呢?总之只能靠自己了吧。
输入数据可以在题目下方的附件中下载。
Input Format
第一行一个正整数 ,表示测试点编号。
若 ,表示 Subtask 1。接下来一行仅一个正整数 。
若 ,表示 Subtask 2。第二行一个正整数 。 接下来 行,第 行先输入一个正整数 ,表示左部分第 个点(记作 )的度数为 ;后面接着 个整数 ,依次表示与 连接的右部分节点编号。
若 ,表示 Subtask 3。第二行输入三个正整数 ,表示输入的初始形态有 行 列(除此之外是无限大的二维平面,没有其它细胞),迭代 次。接下来 行,每行一个长度为 的 01 串,0 表示空地,1 表示细胞,描述了一行的形态。
若 ,表示 Subtask 4。第二行输入三个正整数 。接下来 行,每行两个正整数 描述一条无向边,保证无重边和自环。
Output Format
输出一行一个正整数,表示答案。
3
3
2 1 2
2 2 3
2 1 3
2
7
5 5 133
10001
00000
11111
00000
01010
129
Hint
【样例 解释】
输入中 ,要求的问题是二分图完美匹配计数。
可以发现,只有两种匹配方案:$1 \leftrightarrow 1,2 \leftrightarrow 2,3 \leftrightarrow 3$
或 $1 \leftrightarrow 2,2 \leftrightarrow 3,3 \leftrightarrow 1$。
【样例 解释】
输入中 ,要求的问题是预测生命游戏细胞数。给出的输入是:

经过 轮迭代后为:

可以数出其中细胞数为 。
样例中虽然有 ,但并不代表实际输入。
【测试点分数信息】
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 分数 |

 京公网安备 11011102002149号
京公网安备 11011102002149号