#P8389. [COI 2021] Izvanzemaljci
[COI 2021] Izvanzemaljci
Description
译自 COI 2021 T3「Izvanzemaljci」
在二维平面上有 个整点 ,请找出 个不相交的正方形,使得所有整点在正方形内或在正方形上,如有多解,求出在所有构造方案中面积最大的正方形面积最小的那一种,如果还有多解,输出任意一组即可。
两个正方形如果没有边相交或相碰,并且没有一个正方形完全被另一个正方形包含的情况,则这两个正方形不相交。
Input Format
第一行为两个整数 ,。
接下来 行,一行两个整数 ,。
Output Format
共 行,每行三个整数 ,,,表示有一个左下角为 ,边长为 的正方形。
您需要保证 ,。
3 1
1 1
1 3
2 2
0 1 2
5 2
1 3
3 1
5 5
5 10
7 7
1 1 4
5 7 3
5 3
1 3
3 1
5 5
5 10
7 7
1 1 2
5 5 2
5 10 1
Hint
【样例解释】
样例 #2 解释:

样例 #3 解释:
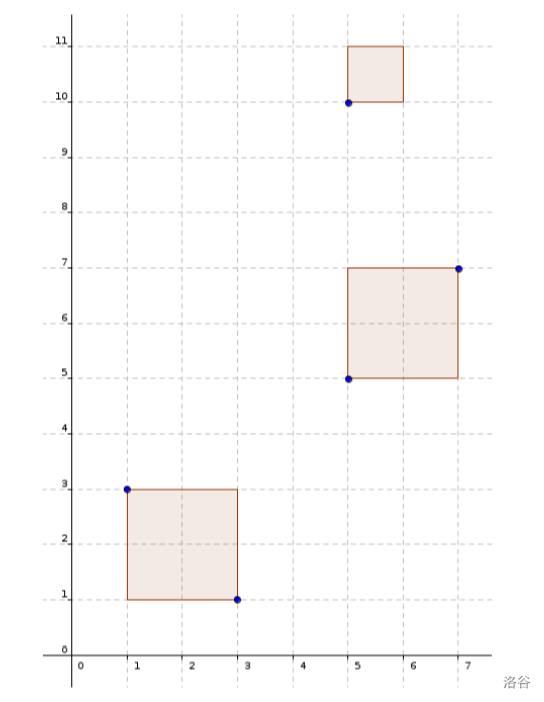
【数据范围】
对于全部数据,有 ,,。
| Subtask | 限制 | 分数 |
|---|---|---|
| , | ||
| , | ||

 京公网安备 11011102002149号
京公网安备 11011102002149号