题目描述

现有一个包含 $n$ 块挡板的旧弹球机。

游戏在二维平面内进行，其中每块挡板与坐标轴所夹锐角总为 $45^\circ$，长度为 $1$ 个单位。挡板用其中心坐标 $(x_i,y_i)$ 和字符 / 或 \ 来表示。小球在碰到挡板后，其运动方向将会旋转 $90^\circ$。注意，挡板的两面都可使小球的运动方向发生偏转。

不难发现，当小球处于弹球机中时，它只有两种结局：

• 沿着某一方向一直运动下去而不碰到挡板
• 处于若干个挡板的循环之中

在翻新弹球机的过程中，有四种颜色的染料可供选择。现要将弹球机中的每个挡板进行染色，使得每一个循环内经过每一种颜色的次数相同且为偶数。

请给出一种符合题意的染色方式，或证明这样的染色方式不存在。如果不存在，输出 -1。

输入格式

第一行一个正整数 $n$，表示挡板的数量。

接下来的 $n$ 行，每行两个正整数 $x_i,y_i$ 和一个字符 $c_i$（/ 或 \），表示一个挡板。数据保证，挡板的位置不会相互重合。

输出格式

如果不存在符合题意的染色方式，输出 -1。

否则输出 $n$ 个整数 $1 \sim 4$，表示 $n$ 个挡板所选择的染料颜色。如果有多种符合题意的方式，输出任意一种。

4
1 1 \
3 1 /
3 2 \
1 2 /

-1

9
1 2 \
1 3 /
2 1 \
2 2 \
2 3 \
3 1 /
3 2 \
4 2 /
4 3 \

1 3 2 4 1 3 2 4 1

12
1 2 \
1 3 /
2 1 \
2 2 \
2 3 \
2 4 /
3 1 /
3 2 \
3 3 \
3 4 \
4 2 /
4 3 \

1 3 2 4 2 4 1 3 1 3 2 4

提示

【样例 2 图解】

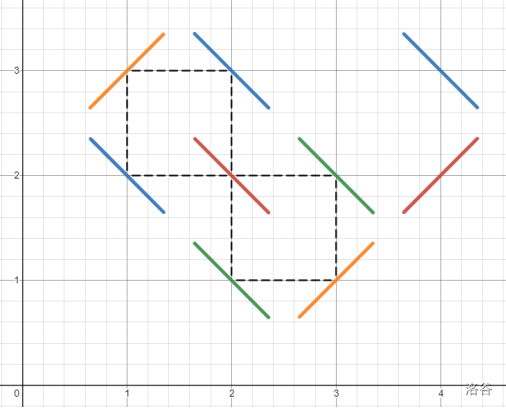
【数据规模与约定】

本题采用捆绑测试。

• Subtask 1（20 pts）：$1 \le n \le 40$。
• Subtask 2（20 pts）：最多存在一个循环。
• Subtask 3（70 pts）：无特殊限制。

对于 $100\%$ 的数据，$1 \le n \le 5 \times 10^5$，$0 \le |x_i|,|y_i| \le 10^9$。

【说明】

本题采用自行编写的 Special Judge。如果对此有疑问或想要 hack，请私信编写者或发帖。

【来源】COCI 2021-2022#5 Task 3 Fliper。