#P8281. 「MCOI-08」Fast Enumeration
「MCOI-08」Fast Enumeration
Description
Technoblade 将 Skyblock 抽象为一张 ()节点 条边的简单有向图。他需要求出该图 所有 哈密尔顿回路,即所有排列 使得 并且 为一个合法路径。
数据保证哈密尔顿回路数量非零并小于 。
数据从所有合法数据随机采样。
Input Format
第一行两个正整数 。
接下来 行,每行两个正整数 。
Output Format
输出若干行;每行输出 个正整数,为一个哈密尔顿回路。按照递增字典序输出。
3 3
1 2
2 3
3 1
1 2 3
4 6
1 3
1 4
2 1
2 3
3 4
4 2
1 3 4 2
5 8
1 2
2 3
3 4
4 1
2 5
4 5
5 1
5 3
1 2 3 4 5
1 2 5 3 4
5 10
1 2
1 3
2 3
2 4
3 4
3 5
4 1
4 5
5 1
5 2
1 2 3 4 5
1 3 5 2 4
6 15
1 3
1 4
1 5
2 1
2 3
2 4
3 1
3 4
4 2
4 6
5 2
5 3
6 1
6 2
6 3
1 5 2 3 4 6
1 5 2 4 6 3
1 5 3 4 6 2
6 15
1 3
1 5
2 1
2 4
3 1
3 2
3 4
3 5
3 6
4 6
5 1
5 4
5 6
6 3
6 5
1 3 2 4 6 5
1 5 4 6 3 2
6 16
1 3
1 6
2 3
2 4
2 6
3 1
3 6
4 2
4 3
4 5
4 6
5 2
5 6
6 1
6 3
6 5
1 6 5 2 4 3
6 21
1 2
1 5
1 6
2 1
2 3
2 4
2 5
3 1
3 2
3 4
3 6
4 1
4 2
4 6
5 1
5 2
5 4
5 6
6 2
6 3
6 4
1 2 5 4 6 3
1 2 5 6 3 4
1 5 2 3 6 4
1 5 2 4 6 3
1 5 4 6 2 3
1 5 4 6 3 2
1 5 6 2 3 4
1 5 6 3 2 4
1 5 6 3 4 2
1 5 6 4 2 3
1 6 3 2 5 4
1 6 3 4 2 5
Hint
样例 1 解释
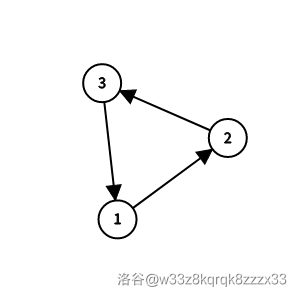
有 个哈密尔顿回路:
- 。
样例 2 解释
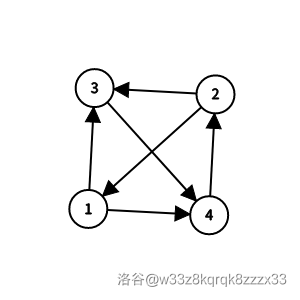
有 个哈密尔顿回路:
- 。
样例 3 解释
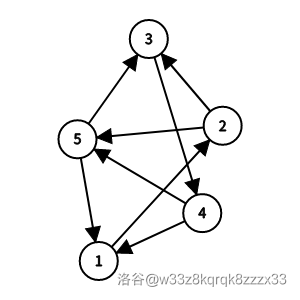
有 个哈密尔顿回路:
- ;
- 。
样例 4 解释
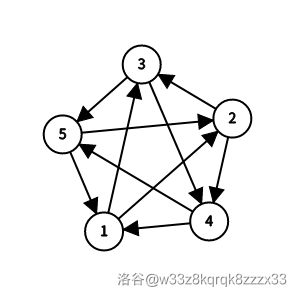
有 个哈密尔顿回路:
- ;
- 。
样例 5 解释
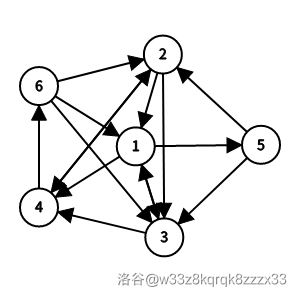
有 个哈密尔顿回路:
- ;
- ;
- 。
样例 6 解释
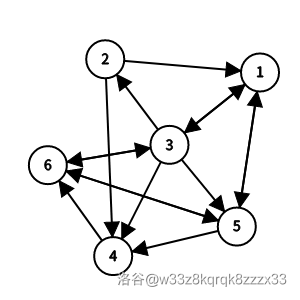
有 个哈密尔顿回路:
- ;
- 。
样例 7 解释
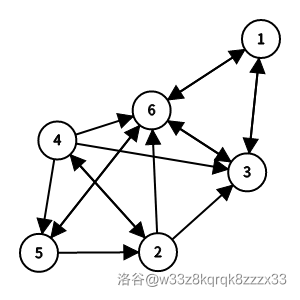
有 个哈密尔顿回路:
- 。
样例 8 解释
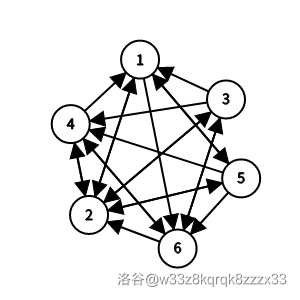
有 个哈密尔顿回路:
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- 。
数据规模与约定
对于固定 和 ,任意一张 条边的图权重为 $\left(\frac{1}{P}\right)^m\left(\frac{P-1}{P}\right)^{n^2-n-m}$。
- Subtask 1(1 pts):为样例。
- Subtask 2(16 pts):。
- Subtask 3(20 pts):。
- Subtask 4(26 pts):。
- Subtask 5(37 pts):。

 京公网安备 11011102002149号
京公网安备 11011102002149号