#P8222. [WFOI - 02] I wanna escape the shadow(阴影)
[WFOI - 02] I wanna escape the shadow(阴影)
Description
现在 kid 身处一个圆心为 ,半径为 的圆中,并且学会了一种新的操作 mklig(X,Y,Z) 来消除黑暗,具体如下:
是三个不同的点,作射线 ,设两条射线与圆周交于 ,那么将 弧 ,线段 围成的区域照亮。
现在圆内有一些点,记 是圆的半径为 的时候被照亮的总面积,现在 kid 想知道在使 (可以理解为 r 无穷大时)最大时,最少需要多少次 mklig 操作。你只需要给出答案,剩下的操作就交给 €€£ 吧!
数据保证不存在三点共线。
Input Format
本题有多组数据
第一行一个整数 ,表示数据组数;
对于每组数据:
第一行一个正整数 ;
接下来 行,每行两个整数,分别表示一个点的横纵坐标。
Output Format
共 行,每行一个整数,表示答案。
1
3
0 0
0 2
-1 1
3
Hint
-
样例解释
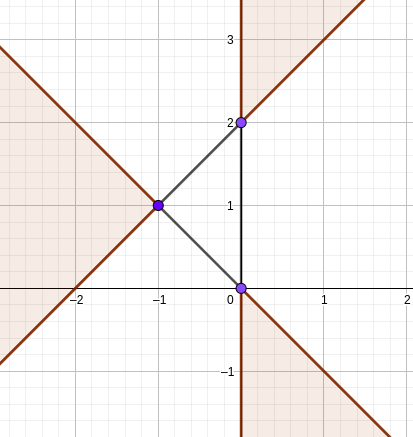
本题采用 Subtask 捆绑测试。
- : 且数据随机;
- : ;
- :;
对于每个测试点,保证 ,点的坐标的绝对值不超过 。

 京公网安备 11011102002149号
京公网安备 11011102002149号