题目背景

译自 CEOI2021 Day2 T3. Wells。

本题数据不全，建议去 loj 提交：https://loj.ac/p/3597 。

题目描述

给出一个有 $N$ 个结点的树和一个正整数 $K$，确定是否存在一个顶点子集，使得任意恰好包含 $K$ 个顶点的路径都恰好有一个来自该子集的顶点。此外，您需要找到模 $10^9+7$ 的此类子集的数量（不存在则为 $0$）。

输入格式

第一行两个整数 $N$ 和 $K$。

接下来 $N-1$ 行，每行两个整数 $u$ 和 $v$，表示节点 $u$ 和节点 $v$ 之间存在一条无向边。

输出格式

第一行一个字符串，如果存在输出 YES，否则输出 NO。

第二行输出一个整数，表示满足条件的子集个数，如果不存在，输出 $0$。

4 2
3 4
3 1
2 3

YES 
2

8 3
7 3
1 3
7 8
5 1
4 6
7 2
3 6

NO
0

6 5
4 1
4 2
3 6
5 2
4 6

YES
10

提示

样例解释1

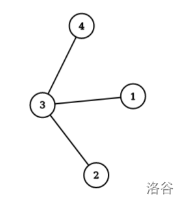
满足条件的子集有：$\{3\}$，$\{1,2,4\}$。

样例解释2

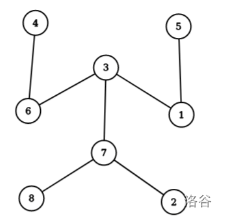
样例解释3

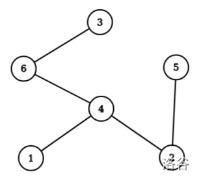
只有一条长度为 $5$ 的路径，该路径包含节点 $3,6,4,2,5$。这些节点中必须恰好有一个在子集中，并且节点 $1$ 是否在子集中没有区别。

因此所有满足条件的子集有：$\{3\}$，$\{1,3\}$，$\{6\}$，$\{1,6\}$，$\{4\}$，$\{1,4\}$，$\{2\}$，$\{1,2\}$，$\{5\}$，$\{1,5\}$。

数据范围与约定

对于 $100\%$ 的数据：$2\leq K\leq N\le 1.5\times 10^6$。

子任务	分值	约束
$1$	$30$	$2\leq K\leq N\le 200$
$2$	$20$	$2\leq K\leq N\le 10^4$
$3$		$2\leq K\leq N\le 5\times 10^5$
$4$	$30$	$2\leq K\leq N\le 1.5\times 10^6$