#P8173. [CEOI 2021] Newspapers
[CEOI 2021] Newspapers
Description
Ankica 和 Branko 在一张无向连通图上玩追逐游戏,游戏分为若干个回合,每一回合有如下两步:
- Ankica 猜测 Branko 现在在哪个结点。具体地,她将猜测 Branko 在某个特定的结点,如果正确,Branko 被抓住,游戏将会结束,否则:
- Branko 穿过一条边。换句话说,Branko将移动到一个相邻的结点,注意他不能不移动。
给出这张图,请求出 Ankica 是否总能在有限步内抓到 Branko 且不论 Branko 初始位置在哪以及如何移动。
更形式化地,我们把 Ankica 猜测的策略用 表示,其中 代表她第 次猜测 Branko 在 结点。
相似地,我们把 Branko 的移动也用 表示,其中 代表他在第 回合前的位置。此外,对于 中任意两个相邻的元素 和 (), 和 之间必定有一条边。注意对于 没有这样的限制。
我们认为 Ankica 的猜测策略 是成功的,当且仅当对于任意合法的 ,都存在 使得 。
如果存在这样的策略,请输出使得 最小的一组策略。
Input Format
输入第一行包含两个整数 和 ,代表这张图的点数和边数。
接下来 行两个整数 ,,表示图上有一条连接 , 的边。
输入保证图上无重边、无自环。
Output Format
如果不存在成功的策略 ,仅输出一行一个字符串 NO。
否则,第一行应输出一个字符串 YES。
第二行应输出该策略最小的 。
第三行应包含 个整数,其中第 个整数表示 。
7 6
1 2
1 3
1 4
1 5
1 6
1 7
YES
2
1 1
6 6
1 2
2 3
3 1
1 4
2 5
3 6
NO
Hint
样例解释1
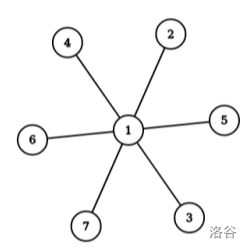
如果 Branko 初始位于 号结点,则他会被抓住,否则他必定会移动到 号结点,然后被抓住。
样例解释2
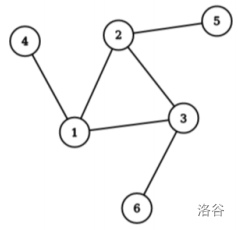
若 Branko 初始在环 上且不与 相同,则根据之后的 必定能构造出使 不合法的 。
子任务
所有测试点均满足 ,。
各子任务的约束条件如下:
| 子任务编号 | 分值 | 限制 |
|---|---|---|
| ,,且每个结点 都与 有边 | ||
评分细则
如果你仅能正确回答第一行,则你将得到该测试点 的分数。
如果对于所有回答 YES 的测试点,你能提供一组 非最小但正确的策略,你将得到该测试点 的分数。注意,你提供的策略不能超过 轮,可以证明,任何一组最优策略都不会超出这个限制。
每个子任务的得分等于该子任务内得分最小的测试点得分。

 京公网安备 11011102002149号
京公网安备 11011102002149号