题目背景

こんな僕が生きてるだけで
何万人のひとが悲しんで
誰も僕を望まない
そんな世界だったらいいのにな
——《自傷無色》

题目描述

给定一棵 $n$ 个节点的树，根节点为 $1$，有边权。约定树上 $u,v$ 两点间路径长度 $d(u,v)$ 为 $u,v$ 间路径上的边权和。

对于一个无序二元组 $(u,v)$，定义一个「树三角」当且仅当同时满足：

• $u,v$ 的最近公共祖先 $w\neq u$ 且 $w\neq v$。
• 以 $d(u,w),d(v,w)$ 和某个正整数 $x$ 为边长，能构成一个三角形。$x$ 是任意选取的，因此一对 $(u,v)$ 可能会产生多个树三角。

此时 $d(u,w)+d(v,w)+x$ 即为这个树三角的大小。具体例子参考样例解释。

定义两个树三角不同，只需满足下列条件中的一条：

• 无序二元组 $(u,v)$ 不同。
• 树三角的大小不同。

对于一个带边权的树 $T$，定义其正弦值 $\sin T$ 为 $T$ 中所有树三角大小的和与 $T$ 中不同树三角总数量的比值。

小 H 给出了 $T$，希望你能求出 $\sin T$。为了避免误差，结果对 $10^9+7$ 取模。特别地，若 $T$ 中不存在树三角，则 $\sin T=0$。

输入格式

第一行，一个正整数 $n$：表示树的节点数。

接下来 $n-1$ 行，每行三个正整数 $u,v,w$：表示节点 $u,v$ 之间有一条权值为 $w$ 的边。

输出格式

共一行，为 $\sin T$ 的值对 $10^9+7$ 取模。数据保证 $T$ 中不同树三角总数量不是 $10^9+7$ 的倍数。

5
1 2 2
1 3 3
2 4 1
2 5 2

214285725

9
1 2 9
1 3 3
2 4 5
2 5 7
2 6 2
1 7 1
3 8 6
3 9 4

662721928

提示

样例解释

对于样例 1，$T$ 如下图所示。

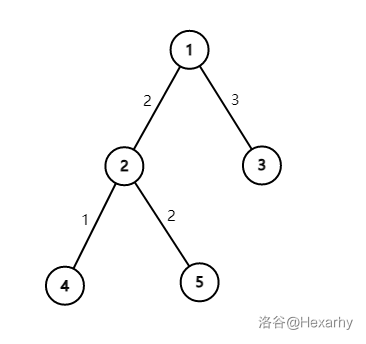
节点 $1,2,3$ 构成的三角环有：$\underline{2,3},2;~\underline{2,3},3;~\underline{2,3},4$。

节点 $1,3,4$ 构成的三角环有：$\underline{3,3},1;~\underline{3,3},2;~\underline{3,3},3;~\underline{3,3},4;~\underline{3,3},5$。

节点 $1,3,5$ 构成的三角环有：$\underline{3,4},2;~\underline{3,4},3;~\underline{3,4},4;~\underline{3,4},5;~\underline{3,4},6$。

节点 $2,4,5$ 构成的三角环有：$\underline{1,2},2$。

所有三角环大小之和：$(7+8+9)+(7+8+\dots+11)+(9+10+\dots+13)+5=129$。

所有三角环的总个数：$3+5+5+1=14$。

$\sin T=\dfrac{129}{14}$，对 $10^9+7$ 取模后的结果为 $214285725$。

数据范围

本题采用捆绑测试。

• 特殊性质 A：保证 $T$ 中存在度为 $n-1$ 的节点。
• 特殊性质 B：保证 $T$ 中除了叶子节点，每个节点的度均为 $2$。
• 特殊性质 C：保证 $T$ 为满二叉树。

Subtask	分值	$1\le n\le$	特殊性质
$1$	$5$	$3$	无
$2$	$13$	$10^3$
$3$	$11$	$7\times10^3$
$4$	$17$	$10^5$	A
$5$			B
$6$			C
$7$	$20$		无

对于 $100\%$ 的数据，$1\le n\le 10^5$，$1\le w\le 10^9$。

提示

在题目附件 depression_sample.zip 中：

• depression_sample1.in 即为样例 #1。
• depression_sample2.in 满足特殊性质 A。
• depression_sample3.in 满足特殊性质 B。
• depression_sample4.in 满足特殊性质 C。
• depression_sample5.in 不满足特殊性质。