题目描述

$\text{Anica}$ 有一张神秘的无限表，表里有无限行和无限列。有趣的是，表中的每个数字出现的次数是有限的。

定义函数 $\mathrm{rev}(i)$，返回 $i$ 在十进制下翻转后得到的新数字。例如 $\mathrm{rev}(213)=312$，$\mathrm{rev}(406800)=008604=8604$。

表中第 $i$ 行第 $j$ 列的数字 $A(i,j)$ 由以下方式得到：

• $A(i,1)=i$

• $A(i, j) = A(i, j − 1)+\mathrm{rev}\big(A(i,j-1)\big)$，$j>1$

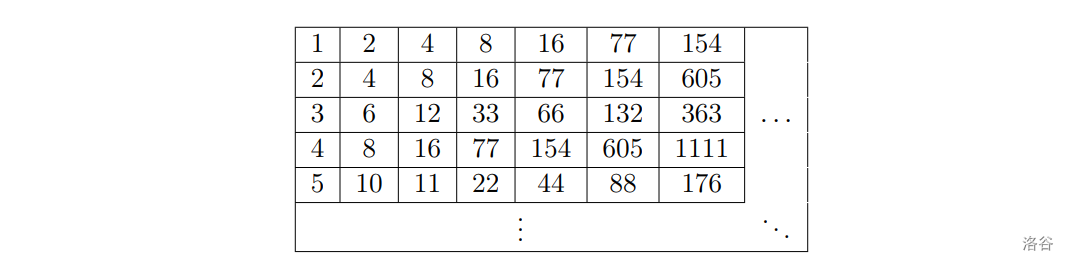
现在 $\text{Anica}$ 给出 $Q$ 个询问，每个询问给出两个整数 $L$ 和 $R$，请你求出无限表中有多少个数的大小在 $\big[L,R\big]$ 中。

输入格式

第一行包含一个整数 $Q$。

接下来 $Q$ 行，每行包含两个整数 $L$ 和 $R$。

输出格式

输出包含 $Q$ 行，每行一个整数，其中第 $i$ 行为第 $i$ 个问题的答案。

2
1 10
5 8

18
8

3
17 144
121 121
89 98

265
25
10

1
1 1000000000

1863025563

提示

【数据范围】

对于 $50\%$ 的数据，保证 $1\le L,R\le 10^6$。

对于 $100\%$ 的数据，保证 $1\le Q\le 10^5$，$1\le L,R\le 10^{10}$。

【题目来源】

题目译自 COCI 2015-2016 CONTEST #6 T6 SAN。

本题分值按 COCI 原题设置，满分 $160$。