#P7592. 数树(2021 CoE-II E)
数树(2021 CoE-II E)
Description
定义一棵树 为 叉树,当且仅当每个节点 有儿子,要么有 个儿子,要么有 个儿子,。我们定义两棵 树同构,当且仅当以下伪代码返回的字符串相同:
$$\begin{array}{ll} 1 & \textbf{Input. } \text{The edges of the tree } \mathcal T \\ 2 & \textbf{Output. } \text{The eigenvalue of tree } \mathcal T.\\ 3 & \textbf{Algorithm. } \text{dfs}(u)\\ 4 & \qquad result \gets \texttt{'('} \\ 5 & \qquad \textbf{for} \text{ each } (u, v) \text{ in the } \mathcal T \\ 6 & \qquad \qquad \textbf{if } v \text{ is not the father of } u \\ 7 & \qquad \qquad\qquad result \gets result\ +\ \mathrm{dfs}(v) \\ 8 & \qquad result\gets result\ +\ \texttt{')'} \\ 9 & \qquad \textbf{return } result \\ 10 & \textbf{Method. } \text{check}(\mathcal T) \\ 11 & \qquad \textbf{return } \text{dfs(the root of the tree } \mathcal T\text{)} \end{array}$$形式化地, 叉树有确定的根节点,每个节点的若干儿子之间有顺序,但是节点没有标号。
若 叉树 有一个 叉节点,则得分 ,若有一个 叉节点,则得分 ,叶节点无得分。定义一棵树的得分为其所有节点的得分之和,记为 。
现在我们在所有互不同构的 个节点的 叉树中等概率随机生成一棵 ,记 的期望值为 。
可以证明 为有理数。当 不为零时,令答案 ,其中 与 互质。你需要输出最小的自然数 使得 ,其中 ,可以证明这样的自然数 必定存在。
Input Format
输入包含五个整数 ,其含义如题目描述所示。
Output Format
输出一个整数 ,表示方程 的最小自然数解,其中 。
2 3 6 1 2
3
Hint
样例说明
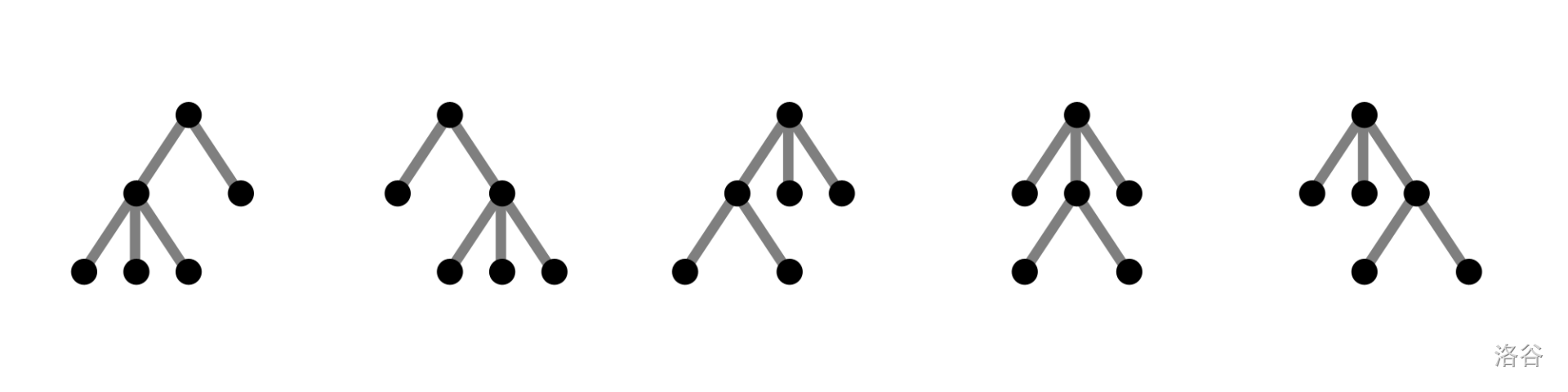
具有 个结点的不同构 叉树共有 棵,每棵得分均为 分,则 ,故 且 ,则 。
数据范围
共 个测试点。
对于测试点 ,满足 。
对于测试点 ,满足 。
对于测试点 ,满足 。
对于测试点 ,满足 。
对于 的数据,满足 $1 \le k_1,\ k_2<n\leq 10^7,\ k_1 \ne k_2, \ k_1+k_2 \le n, \ \ 1 \le \ a,\ b\leq 10^7$。
约定
- 测试数据保证 不为零。

 京公网安备 11011102002149号
京公网安备 11011102002149号