题目背景

“原来如此，这就是你欲望的根本吗，真有意思呢…”

声音在墓穴中传开来，昴猛然回头，眼前的景象却骤然大变：他的四周由昏黑的墙壁变为了一望无际的草坪，起伏着大大小小的山丘；而原本应该是墓穴入口的地方，却有着一张茶桌和两张座椅，与之一齐处在遮阳伞的荫庇下的，还有一位端坐着的黑衣女子。

“我好久没有跟人类对话了，就兴奋了点… 我叫艾姬多娜。「强欲魔女」，这样说比较好懂吧？” 女子浅笑着说道。

“… 这是哪里！？我应该在一个黑暗的遗迹中，你是什么时候把我转移过来的？” 昴咬紧了牙，问道。

“很遗憾，你搞错了。你并不是肉体经历了转移，只是被邀请参加我的茶会而已。”

“茶会…？”

“是魔女的茶会哦。”

[管理员 Mivik 更改了时间线]

题目描述

“那么… 你还准备在那里站多久？趁着茶还没凉赶紧入座吧。”

“可恶… 知道啦知道啦！” 昴走上前去，坐在了魔女对面。桌上除了两杯茶外，还有一副黑白交错的棋盘。

“这是…？” 昴指着棋盘，问道。

“这是魔女棋哦。我请你过来是为了解答我沉思多年都无法解决的一个问题。如果你解决了它，我就会给你和爱蜜莉雅参加试炼的权利… 否则…”令人不安的笑容浮现在魔女脸上，“你可能就会在圣域里无穷地轮回哦…？”

昴出了一身冷汗，战战兢兢地问道：“那么问题是？”

魔女拾起了身边的一个棋子，缓缓说道：“如你所见，这是一张 $n\times n$ 的棋盘，由 $n^2$ 个方格组成，每个方格上最多只能存在一个棋子。不同于普通的棋盘，这个棋盘是循环的，也就是说，第 $i$ 行 $n$ 列的格子右边是第 $i$ 行 $1$ 列的格子，第 $n$ 行 $i$ 列的格子下面是第 $1$ 行 $i$ 列的格子，以此类推。 我手中的棋子名叫「大罪司教」，它一步可以向任意斜线方向移动任意多格。一个棋子能一步走到的格子称为其掌控的格子。如果一个棋子掌控了另一个棋子所在的方格，则这种棋盘布局是不稳定的，反之称其为稳定的。现在，请问你能否向棋盘中放入恰好 $m$ 个「大罪司教」，使得整个棋盘布局是稳定的呢？”

上图高清版

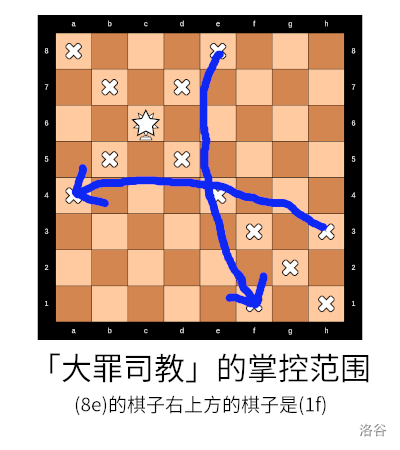
昴沉思了一会儿，随后在棋盘上操作，很快就完成了魔女的任务，说道：“那么快给我参加试炼的权利吧！”

魔女说：“不行啦… 我还有一个问题没有解决呢…”

昴：“靠北，你耍赖啊！”

魔女没有理会昴，继续说道：“现在问题是，一共有多少种本质不同的稳定的布局方案，使得布局中恰好有 $m$ 个「大罪司教」呢？两种方案本质不同，当且仅当存在任意一格在一种方案中有棋子而在另一种方案中没有哦。”

昴更加生气，因为他不会做了，他转而求助于你。你只需要告诉他答案对 $998244353$ 取模的结果即可。

输入格式

一行两个正整数 $n,m$，代表棋盘的大小和你需要放置的棋子数目。

输出格式

一行一个正整数，代表答案对 $998244353$ 取模的结果。

1 1

1

2 2

4

3 2

18

10 5

8647680

提示

样例一：将一个棋子放入 $1\times1$ 的棋盘中显然只有一种方案。

样例二：一共有以下四种稳定的布局（用 . 代表空位，o 代表「大罪司教」）：

oo .o .. o.
.. .o oo o.

样例三：所有 $18$ 种稳定的布局可以在 这里 查看。

数据范围

对于全部数据，有 $1\le n<998244353$，$0\le m\le\min\{n,10^7\}$。

Subtask 1 (5 pts)：保证 $m=0$。

Subtask 2 (10 pts)：保证 $m=1$。

Subtask 3 (10 pts)：保证 $1\le n\le 4$。

Subtask 4 (20 pts)：保证 $n$ 是奇数。

Subtask 5 (25 pts)：保证 $n\le 10^7$。

Subtask 6 (30 pts)：无特殊限制。