题目描述

有一个 $n$ 行 $n$ 列的正方形点阵，左上角点坐标为 $(1, 1)$，右下角点坐标为 $(n, n)$。

点阵中每个整点上都有数量不一的豆子，坐标为 $(i, j)$ 的点上有 $a_{i,j}$ 个豆子。

你可以放置吃豆人，可以将点阵中任意的整点作为吃豆人的初始位置，再给定左上、左下、右上、右下之一作为吃豆人的初始方向。

吃豆人会不断沿初始方向行进，吃光遇到的所有豆子，直到碰到点阵的边界，此时：

1. 如果吃豆人处于正方形点阵四个角之一的位置，那么就会停止行动；

2. 否则，吃豆人的行进路线将以这条边界为镜面发生反射，下图展示了一个路径某两次发生反射的例子：

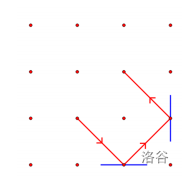
现在，你需要放置两个吃豆人，求两个吃豆人最多共能吃到多少个豆子？注意同一个豆子只能被吃一次。

输入格式

第一行包含一个整数 $n$，表示点阵大小。

接下来 $n$ 行，每行包含 $n$ 个整数，其中第 $i$ 行第 $j$ 个整数表示 $a_{i,j}$。

输出格式

输出一行一个整数，表示两个吃豆人最多共能吃到的豆子数量。

4
20 1 19 2
3 18 4 17
16 5 15 6
7 14 8 13

132

提示

样例 1 解释

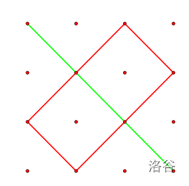
在 $(1, 1)$ 和 $(1, 3)$ 位置放置吃豆人，初始方向分别为右下和左下，即可吃到位于 $(1, 1)$，$(1, 3)$，$(2, 2)$，$(2, 4)$，$(3, 1)$，$(3, 3)$，$(4, 2)$，$(4, 4)$ 位置上的豆子，总个数为 $132$， 达到最大，路径分别如下图绿线和红线所示：

数据范围

对于 $30\%$ 的数据，$n\leq 3$。

对于 $60\%$ 的数据：$n\leq 100$。

对于 $100\%$ 的数据：$2\leq n\leq 1000$，$0\leq a_{i,j}\leq 1000$。

数据由 SSerxhs 和 Karry5307 共同提供。

感谢 Silence_water 提供一组 hack 数据。