题目描述

现有一座上下起伏的山。它可以抽象为一个包含 $n$（$n$ 为奇数）个点 $(x_i,y_i)$ 以及 $(x_1,-\inf)$ 与 $(x_n,-\inf)$ 的多边形。

对于所有满足 $i \neq 1$，$i \neq n$，$i \bmod 2=1$ 的整数 $i$，$(x_i,y_i)$ 都是山谷。

现要放置若干个高度为 $h$ 的点光源，使得所有的山谷都被照亮，即点光源与山谷的连线不经过山的内部。

求所需点光源的最少数量。

输入格式

第一行输入整数 $n,h$。

接下来的 $n$ 行，每行输入整数 $x_i,y_i$。

保证 $x_1 \lt x_2 \lt \cdots \lt x_n$ 且 $y_1 \lt y_2,y_2 \gt y_3,y_3 \lt y_4,\cdots,y_{n-1} \gt y_n$。

输出格式

输出所需点光源的最少数量。

9 6
0 0
1 2
3 0
6 3
8 1
9 2
11 1
12 4
14 0

1

9 5
-5 2
-4 3
-2 1
0 4
2 2
3 3
4 1
5 2
6 1

2

提示

样例 1 图解

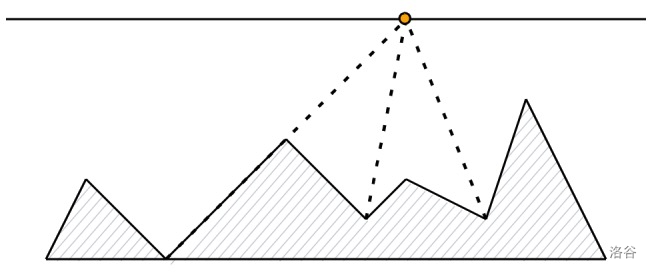
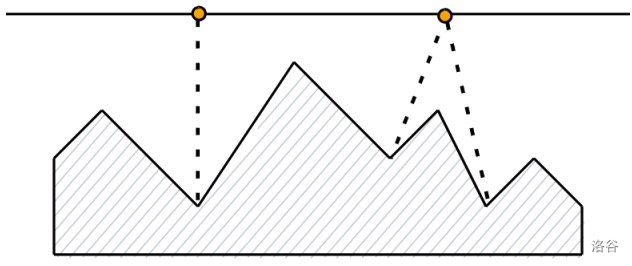
样例 2 图解

数据规模与约定

本题采用捆绑测试。

对于 $100\%$ 的数据，$3 \le n \lt 10^6$，$n \bmod 2=1$，$1 \le h \le 10^6$，$-10^6 \le x_i \le 10^6$，$0 \le y_i \lt h$，$x_1 \lt x_2 \lt \cdots \lt x_n$，$y_1 \lt y_2,y_2 \gt y_3,y_3 \lt y_4,\cdots,y_{n-1} \gt y_n$。

说明

本题分值按 COCI 原题设置，满分 $110$。

题目译自 COCI2020-2021 CONTEST #5 T4 Planine。