#P7283. [COCI 2020/2021 #4] Janjetina
[COCI 2020/2021 #4] Janjetina
Description
Malnar 先生将访问 个城市,分别用整数 到 表示。同时,他经过调研发现,有 条连接其中两个城市的双向路。
每条路上均有一家提供羊肉的餐厅,同时给定每个餐厅可以订购的最大羊肉的重量。
他将选择两个城市 和 ,并以最短路径(指经过的最少的路)从 到达 。他将且仅将在一家餐厅停留,且这家餐厅为可提供羊肉重量最多的一家(如果有多家这样的餐厅,他将会选择任意一家),并将订购的羊肉全部吃光。
如果通过一种长度为 的路径可以吃到 千克的羊肉,且 ,那么 Malnar 先生就称之为满意的。一种路径的长度等同于其经过路的条数。
求有多少个有序数对 ,使得从 到 的最短路径是满意的。
Input Format
第一行输入整数 ,其中 表示城市的个数。
接下来的 行,每行输入三个整数 ,表示有一条连接城市 的路,且这条道路有一家提供 千克羊肉的餐厅。
Output Format
输出满足题意的有序数对的个数。
3 1
1 2 3
1 3 2
6
4 1
1 2 1
2 3 2
3 4 3
6
5 2
1 2 2
1 3 3
3 4 2
3 5 4
8
Hint
样例 1 解释
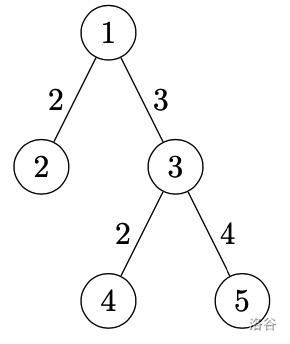
满足题意的有序数对有 。
数据规模与约定
本题采用捆绑评测。
| Subtask | 分值 | 数据范围及约定 |
|---|---|---|
| 城市 和 ()直接相连(即最短距离为 ) | ||
| 无 |
对于 的数据,,。
说明
本题分值按 COCI 原题设置,满分 。
题目译自 COCI2020-2021 CONTEST #4 T4 Janjetina。

 京公网安备 11011102002149号
京公网安备 11011102002149号