题目背景

杰瑞米是一个牛蛙，是我的一个好朋友。

题目描述

有 $n$ 片百合花，它们分别从 $1$ 到 $n$ 依次编号。第 $i$ 片上有一个整数 $x_i$，而序列 $(x_i)_{1 \le i \le n}$ 单调递增。

三只青蛙到来。

每对满足 $a \lt b$ 的百合 $(a,b)$ 必须属于青蛙 $1,2$ 或 $3$ 中的其中一只。

当百合 $(i,j)$ 属于一只青蛙且 $x_j$ 能被 $x_i$ 整除时（$j \gt i$），该青蛙可以从 $i$ 号百合跳动到第 $j$ 号。

请找出一种分类方案，使得任何一只青蛙都不会连续跳动 $3$ 次。

输入格式

第一行输入一个正整数 $n$，表示百合花的数量。

第二行输入 $n$ 个正整数 $x_i$，表示百合花上的整数。

输出格式

输出 $n-1$ 行。第 $i$ 行输出 $i$ 个整数，其中该行第 $j$ 个整数表示 $(j,i+1)$ 所归属的青蛙。

8
3 4 6 9 12 18 36 72

1
2 3
1 2 3
1 2 3 1
2 3 1 2 3
1 2 3 1 2 3
1 2 3 1 2 3 1

2
10 101

1

提示

样例 1 解释

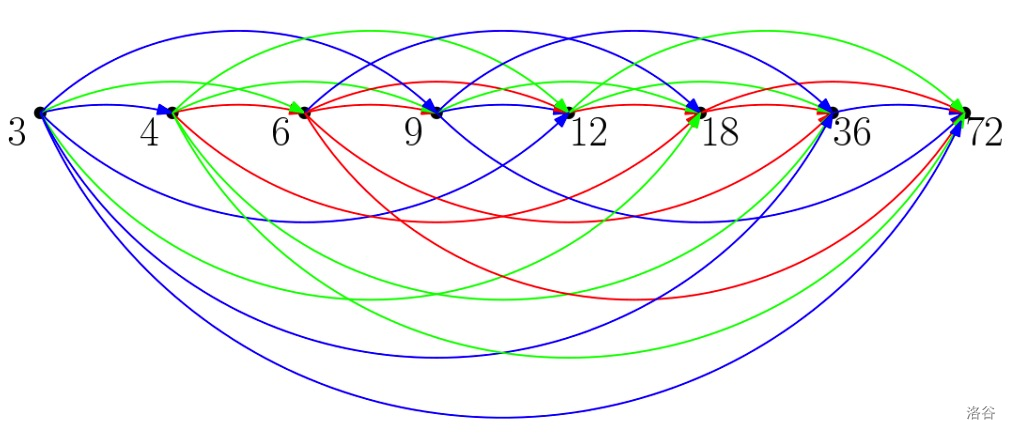
青蛙 $1,2,3$ 分别用蓝、绿和红色代替。

蓝蛙可以从 $x_1=3$ 跳动到 $x_4=9$，再跳动到 $x_7=36$，再到 $x_8=72$。该青蛙只能进行 $3$ 次连续的跳动。

绿蛙可以从 $x_2=4$ 跳动到 $x_5=12$，再跳动到 $x_7=36$。该青蛙只能进行 $2$ 次连续的跳动。

红蛙不能从 $x_2=4$ 跳动到 $x_3=6$，因为 $6$ 不能被 $4$ 整除。

数据规模与约定

本题采用捆绑评测。

Subtask	分值	数据范围及约定
$1$	$10$	$n \le 30$
$2$	$100$	无

对于 $100\%$ 的数据，$1 \le n \le 1000$，$1 \le x_i \le 10^{18}$。

评分方式

在输出方案中，如果其中一只青蛙可以连续跳动 $k$ 次，其中 $k \gt 3$，而没有青蛙可以连续跳动 $k+1$ 次，则对应测试点的分数为 $f(k)·x$ 分，其中：

$$f(k)=\dfrac{1}{10}· \begin{cases} 11-k & (4 \le k \le 5) \cr 8-\lfloor {\dfrac{k}{2}} \rfloor & (6 \le k \le 11) \cr 1 & (12 \le k \le 19) \cr 0 & (k \ge 20) \cr \end{cases}$$

而 $x$ 为对应子任务的总分。每个子任务的得分等于该子任务中所有测试点得分的最小值。

因本题的评分方式特殊，因而启用非官方的自行编写的 Special Judge，也可以在附件中下载。欢迎大家 hack（可私信或直接发帖）。

说明

本题分值按 COCI 原题设置，满分 $110$。

题目译自 COCI2020-2021 CONTEST #4 T3 Hop。