题目背景

您可以在此处下载输入文件。

题目描述

阿塞拜疆因地毯而闻名。作为一位地毯设计大师，你在做新设计时想画一条折线。一条折线是二维平面上包含 $t$ 条线段的线段序列，而这些线段由包含 $t+1$ 个点 $p_0,\ldots,p_t$ 的点序列按照下述规则定义给出：对所有的 $0\le j\le t- 1$，都有一条线段连接点 $p_j$ 和 $p_{j+1}$。

为完成这个新设计，你已经标出了二维平面中的 $n$ 个小圆点。小圆点 $i$（$1 < i < n$）的坐标为 $(x_i,y_i)$。不存在 $x$ 坐标或 $y$ 坐标相同的两个小圆点。

现在你想要找到一个点序列 $(sx_0,sy_0),(sx_1, sy_1)\ldots (sx_k, sy_k)$，由该点序列定义给出的折线需满足：

• 该折线从 $(0,0)$ 开始（即 $sx_0=0$ 且 $sy_0=0$），
• 该折线经过所有的小圆点（它们不必是线段的端点），以及
• 该折线仅包括水平线段和竖直线段（对于定义该折线的连续两个点，其 $x$ 坐标或 $y$ 坐标相等）。

折线可以以任意的方式自相交或自重叠。正式地来说，平面上的每个点可以属于折线中任意数量的线段。

本题是一个有部分分的提交答案型题目。将会给你 $10$ 个输入文件， 这些文件给出了小圆点的位置。对每个输入文件，你需要提交一个答案文件，描述满足要求的折线。对每个给出合法折线的输出文件，你的得分将依赖于折线中的线段数量（参见下面的计分方式一节）。

你不需要为本题提交任何源代码。

输入格式

每个输入文件的格式如下：

• 第 $1$ 行：$n$。
• 第 $1+i$ 行（这里 $1<i\le n$）：$x_i\ y_i$。

输出格式

每个输出文件必须按照如下格式：

• 第 $1$ 行： $k$。
• 第 $1+j$ 行（这里 $1\le j\le k$）： $sx_j\ sy_j$。

注意，第二行应包含 $sx_1$ 和 $sy_1$ （也就是说，输出不应当包含 $sx_0$ 和 $sy_0$）。所有的 $sx_j$ 和 $sy_j$ 均应为整数。

4
2 1 
3 3
4 4
5 2

6
2 0
2 3
5 3
5 2
4 2
4 4

提示

样例解释

这个样例并不是任何一个数据，仅仅只是为了帮助您理解题意。

输出也仅仅是一个可能的输出。

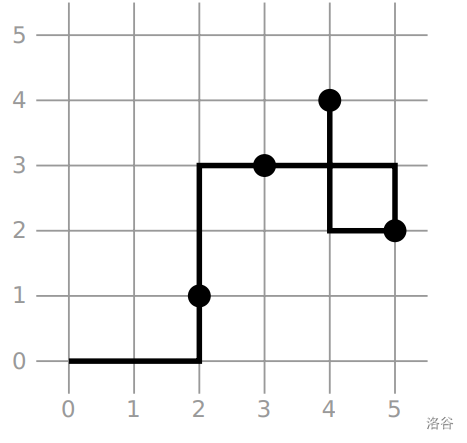
限制条件

• $1\le n\le 10^5$。
• $1\le x_i,y_i\le 10^9$。
• 所有 $x_i$ 和 $y_i$ 的值都是整数。
• 不存在 $x$ 坐标或 $y$ 坐标相同的两个小圆点，也就是说，对于所有的 $i_1\not=i_2$，都有 $x_{i_1}\not=x_{i_2}$ 且 $y_{i_1}\not=y_{i_2}$。
• $-2\times 10^9\le sx_i,sy_j\le 2\times 10^9$。
• 提交的每个文件（无论是输出文件还是压缩文件）的大小均不能超过 $\text{15MB}$。

计分方式

对每个测试点，你最多能够得到 $10$ 分，如果给出一条非法的折线，你将得到 $0$ 分。否则，得分将根据一个递减序列 $c_1, \cdots, c_{10}$ 来计算。

假设你的解答是一条包含 $k$ 条线段的合法折线。那么，你将得到

• $i$ 分，如果 $k=c_i$（$1 \le i \le 10$）
• $i+\dfrac{c_i-k}{c_i-c_{i+1}}$ 分，如果 $c_{i+1} < k < c_i$（$1 \le i \le 9$）
• $0$ 分，如果 $k > c_1$
• $10$ 分，如果 $k < c_{10}$。

可以这样理解：在 $k \in (c_{i+1}, c_i)$ 这个区间上，你的得分是随着 $k$ 减小线性增大的。一旦得分，得分一定在 $[1, 10]$ 区间内。

以下是每个测试点 $n$ 与 $c_i$ 的信息：

测试点	$n$	$c_1$	$c_2$	$c_3$	$c_4$	$c_5$	$c_6$	$c_7$	$c_8$	$c_9$	$c_{10}$
$1$	$20$	$50$	$45$	$40$	$37$	$35$	$33$	$28$	$26$	$25$	$23$
$2$	$600$	$1\ 200$	$937$	$674$	$651$	$640$	$628$	$616$	$610$	$607$	$603$
$3$	$5\ 000$	$10\ 000$	$7\ 607$	$5\ 213$	$5\ 125$	$5\ 081$	$5\ 037$	$5\ 020$	$5\ 012$	$5\ 008$	$5\ 003$
$4$	$50\ 000$	$100 \ 000$	$75\ 336$	$50\ 671$	$50\ 359$	$50\ 203$	$50\ 047$	$50\ 025$	$50\ 014$	$50\ 009$	$50\ 003$
$5$	$72\ 018$	$144\ 036$	$108\ 430$	$72\ 824$	$72\ 446$	$72\ 257$	$72\ 067$	$72\ 044$	$72\ 033$	$72\ 027$	$72\ 021$
$6$	$91\ 891$	$183\ 782$	$138\ 292$	$92\ 801$	$92\ 371$	$92\ 156$	$91\ 941$	$91\ 918$	$91\ 906$	$91\ 900$	$91\ 894$
$7$	$100\ 000$	$200\ 000$	$150\ 475$	$100\ 949$	$100\ 500$	$100\ 275$	$100\ 050$	$100\ 027$	$100\ 015$	$100\ 009$	$100\ 003$

可视化工具

在本题的附加文件中有一个脚本，能让你对输入文件和输出文件进行可视化。

在对输入文件做可视化时，使用如下命令：

python vis.py [input file]

对于某个输入数据，你还可以使用下面的命令对你的解答进行可视化，由于技术方面的限制，所提供的可视化工具仅显示输出文件中的前 $1000$ 条线段。

python vis.py [input file] --solution [output file]

例如：

python vis.py examples/00.in --solution examples/00.out