Description

我们将题目背景中的问题简化。给出 $n$ 个点，以及任意两个点 $i,j$ 之间存在一条无向边的概率 $p_{i,j}$，求图中联通块个数的期望。

Input Format

第一行一个数 $n$。
第二行到第 $n+1$ 行，每行 $n$ 个实数，代表 $p_{i,j}$。测试数据保证对任意 $1\le i \le n$，$p_{i,i}=0$，对任意 $1\le i,j \le n$，$p_{i,j}=p_{j,i}$，$0\le p_{i,j}\le1$ ，输入的实数小数点后位数不超过 $3$ 位。

Output Format

仅一行一个实数，表示连通块个数的期望。当你的答案与标准答案的绝对误差不超过 $10^{-4}$ 时算作正确。

3
0 0.5 0.5
0.5 0 0.5
0.5 0.5 0

1.625000

4
0 0.129 0.58 0.37
0.129 0 0.22 0.134
0.58 0.22 0 0.6
0.37 0.134 0.6 0

2.143266

Hint

样例解释1：以下八种情况出现概率都是 $\dfrac{1}{8}$。

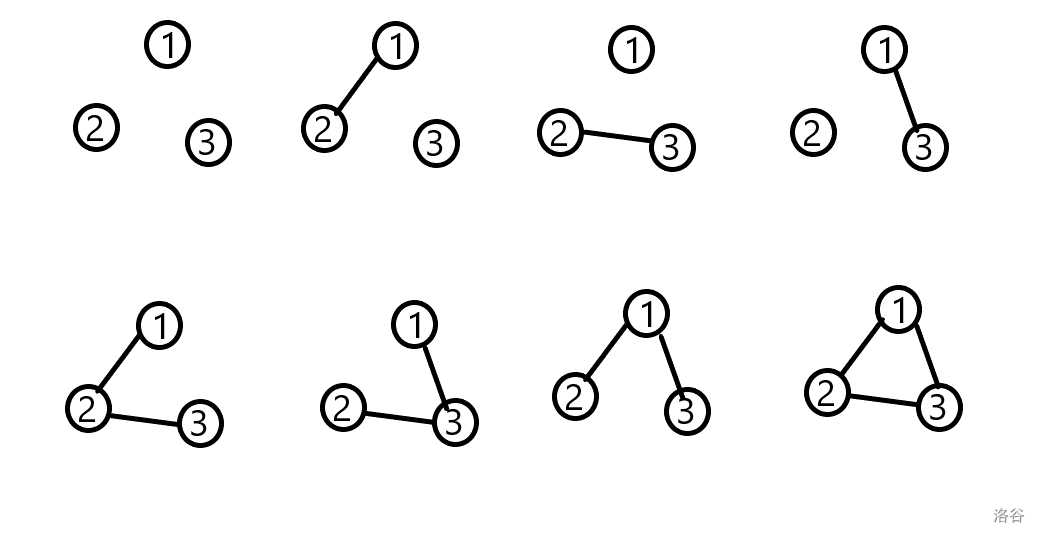
连通块的个数分别为 $3,2,2,2,1,1,1,1$。
所以期望是 $\dfrac{1}{8}\times3+\dfrac{3}{8}\times2+\dfrac{4}{8}\times1=\dfrac{13}{8}=1.625$