题目描述

有一棵树，含 $n$ 个节点，边带权。

会有 $q$ 次修改，每次会将树上的一条边的边权进行修改，在每次修改后，您需要求出每次修改后，这棵树的直径上的边权和。

本题强制在线。

输入格式

第一行为三个整数 $n,q,w$，分别表示点的个数，询问的个数和边权的上限。

接下来 $n-1$ 行，每一行为三个整数 $a_i,b_i,c_i$，表示 $a_i$ 到 $b_i$ 有一条边权为 $c_i$ 的边。

接下来 $q$ 行，每行两个经过加密的整数 $d_j,e_j$。

解密方式如下：

• $d_j'=(d_j+\text{last})\bmod(n-1)$
• $e_j'=(e_j+\text{last})\bmod w$

其中 $\text{last}$ 表示上一个询问的答案，初值为 $0$。

表示将第 $d_j'+1$ 条边的边权改为 $e_j'$。

输出格式

共输出 $q$ 行，一行一个整数，第 $i$ 行的整数表示在第 $i$ 次修改后的直径上的权值总和。

4 3 2000
1 2 100
2 3 1000
2 4 1000
2 1030
1 1020
1 890

2030
2080
2050

10 10 10000
1 9 1241
5 6 1630
10 5 1630
2 6 853
10 1 511
5 3 760
8 3 1076
4 10 1483
7 10 40
8 2051
5 6294
5 4168
7 1861
0 5244
6 5156
3 3001
8 5267
5 3102
8 3623

6164
7812
8385
6737
6738
7205
6641
7062
6581
5155

提示

样例 1 解释

解密后的修改如下：

2 1030
0 1050
2 970

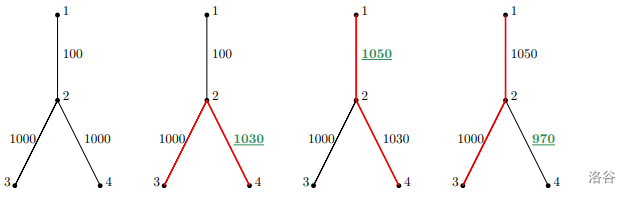
如图为树的边权变化过程，红边代表树的直径：

数据范围

对于 $100\%$ 的数据，保证 $2\le n\le 10^5$，$1\le q\le 10^5$，$1\le w\le 2\times 10^{13}$，$1\le a_i,b_i\le n$，$0\le c_i,e_j<w$，$0\le d_j<n-1$。

详细子任务限制及分值如下表：

说明

本题译自 Central-European Olympiad in Informatics 2019 Day 1 T2 Dynamic Diameter。