#P6835. [Cnoi2020] 线形生物
[Cnoi2020] 线形生物
Description
线形生物要从 号台阶走到 号台阶。
最开始, 号台阶都有一条连向下一台阶的有向边 。
之后 Cirno 加入了 条返祖边 ,它们构成了一个返祖图。
线形生物每步会 等概率地 选取当前台阶的一条出边并走向对应的台阶。
当走到 号台阶时,线形生物就会停止行走。
同时,Cirno 会统计线性生物总共走的步数,记作 。
Cirno 想知道 (即 的数学期望)对 取模后的结果。
Input Format
第一行三个整数 ,,。
以下 行,每行两个整数 ,。
表示 subtask 编号,其它字母含义同上文。
Output Format
一行,一个整数 ,字母含义同上文。
1 5 5
1 1
2 2
3 3
4 4
5 5
10
2 5 5
1 1
2 1
3 2
4 3
5 4
30
3 5 5
1 1
2 1
3 1
4 1
5 1
62
4 5 5
1 1
3 1
4 2
5 1
5 5
35
Hint
后置数学知识
- 可能用到的幂级数求和 : 若 ,则有 $\sum\limits_{i=1}^{\infty}\big(\frac{1}{x}\big)^i=\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x^3}+\cdots=\frac{1}{x-1}$。
- 数学期望 : 随机试验中每次可能结果的概率乘以其结果的总和,反映随机变量平均取值的大小。
- 离散期望公式 : 。
数据范围与约定
对于 的数据,保证:,,。
子任务「本题采用捆绑测试」
-
Subtask1(): 返祖图中所有点都有自环且所有边均为自环(未画出),总图形如 :

-
Subtask2(): 返祖图中所有点均向且仅向自己的前驱连边,特别地, 号节点的前驱是 号节点,总图形如 :

-
Subtask3(): 返祖图中所有点均向且仅向 号节点连边,总图形如 :
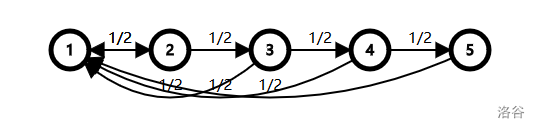
-
Subtask4(): ,。
-
Subtask5(): 无特殊限制。
后记
题目名称出自 th17 东方鬼形兽 6 Boss 埴安神袿姬 Hard / Lunatic 难度符卡 線形「リニアクリーチャー」。

 京公网安备 11011102002149号
京公网安备 11011102002149号