#P6830. [IOI 2020] 连接擎天树
[IOI 2020] 连接擎天树
Description
滨海湾花园是新加坡的一个大型自然公园。公园内有 个塔,称之为“擎天树”。这些塔的编号为 到 。我们希望建立一个桥的集合(桥的数目大于等于 )。每⼀座桥连接两个不同的塔,而且可以双向通行。没有两座桥连接相同的一对塔。
一条从塔 到塔 的路径是一个满足以下条件的塔序列(塔的数目大于等于 ):
- 序列的第一个元素是 ,
- 序列的最后一个元素是 ,
- 序列中所有元素互不相同,
序列中每两个相邻元素(塔)都是被某一座桥连接起来的。
注意根据定义,一个塔到它自己有且仅有一条路径,并且从塔 到塔 的不同路径的数目和从塔 到塔 的不同路径的数目是一样的。
负责该项设计的首席设计师希望待建造的桥梁要符合:任意给定 ,恰好有 条从塔 到塔 的不同路径,其中 。
请构造一个桥的集合来满足设计师的要求,或判定这样的桥梁集合不可能存在。
实现细节
你需要实现下面的这个函数:
int construct(std::vector<std::vector<int> > p)
- :⼀个表示设计师要求的 数组。
- 如果这个建设方案是存在的,该函数应该恰好调用一次
build(见下文)来给出建设方案,然后应返回 。 - 否则,该函数应该返回 ,并且不要调用
build。 - 该函数将被调用恰好一次。
函数 build 定义如下:
void build(std::vector<std::vector<int> > b)
- :一个 的数组, 表示有一座桥连接塔 和塔 ,否则 。
- 注意该数组必须满足:对所有 ,;并且对所有 ,。
Hint
样例说明
例 1
考虑以下调用:
construct([[1, 1, 2, 2], [1, 1, 2, 2], [2, 2, 1, 2], [2, 2, 2, 1]])
这表明从塔 到塔 恰好有一条路径。对于所有其他的塔对 , 恰好有两条不同的路径连接塔 和塔 。这可以通过建设 座桥来实现:连接塔对 和 。
为了给出这个解决方案,函数 construct 应该做以下调用:
build([[0, 1, 0, 0], [1, 0, 1, 1], [0, 1, 0, 1], [0, 1, 1, 0]])
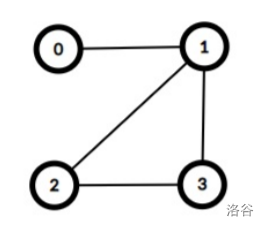
函数应该返回 。
对于这个例子,存在多种不同的建设方案来满足要求,所有这些方案都被认为是正确的。
例 2
考虑以下调用:
construct([[1, 0], [0, 1]])
这表明无法在两个塔之间进行旅行。这只能通过不建设桥梁来满足。
因此,函数 construct 应该做以下调用:
build([[0, 0], [0, 0]])
然后,函数 construct 应该返回 。
例 3
考虑以下调用:
construct([[1, 3], [3, 1]])
这表明从塔 到塔 恰好有 条路径。这些要求无法满足。因此,函数 construct 应该返回 并且不要调用 build。
约束条件
- (对所有 )
- (对所有 )
- (对所有 )
子任务
- (11 分)(对所有 )
- (10 分)(对所有 )
- (19 分)(对所有 )
- (35 分)(对所有 )并且至少有一种建设方案满足要求
- (21 分)(对所有 )
- (4 分)没有额外约束条件
评测程序示例
评测程序示例以如下格式读取输入数据:
第 行:
第 行():
评测程序示例的输出格式如下:
第 行: construct 的返回值。
如果 construct 的返回值为 ,评测程序示例会额外打印:
第 行():

 京公网安备 11011102002149号
京公网安备 11011102002149号