题目背景

1.3s，64MB

题目描述

象棋世界是一个 $R$ 行 $C$ 列的棋盘，其中 $R \geq C$。所有的行依此编号为 $1$ 到 $R$，所有的列依此编号为 $1$ 到 $C$。

在象棋世界里，共有五种棋子：兵，车，象，后，王。与现实世界不同的是，骑士精神在象棋世界中已经死亡，因此象棋世界里找不到马。

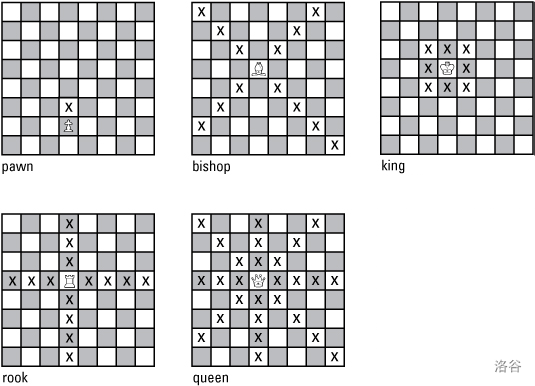
象棋世界里，每种棋子可以按如下规则进行一步移动：

• 兵只能向行号增大的方向走一步（从第 $r$ 行到第 $r+1$ 行），且其所处的列不变。
• 车只能沿水平方向或竖直方向移动。
• 象只能沿对角线方向移动。
• 后可以沿水平方向，竖直方向，或对角线方向移动。
• 王可以向与之相邻的八个格子移动。

为了方便你理解，我们在下图给出了每种棋子的合法移动范围。其中 X 代表该棋子能移动到的位置。

最近一段时间，象棋世界发生了不少诡异的事情：某些棋子可能会被不明来源的力量所劫持，随后从象棋世界中消失。在这种情况下，所有棋子都希望能尽快前往他们想要到达的目的地，他们还想知道，在走的步数最少的前提下，到达目的地的方案数有多少。两种方案是不同的，当且仅当这两种方案中有一步经过的格子不同。

在本题中，你需要解决下面这个问题：某个棋子将从第 $1$ 行的第 $c_1$ 列出发，到达第 $R$ 行的第 $c_R$ 列。现在给出这个棋子的类型，以及 $c_1,c_R$ 的值，你需要求出，这个棋子最少需要走多少步，以及在步数最少的前提下，行走方案有多少种。

输入格式

第一行包含三个整数 $R,C,Q$，表示象棋世界中棋盘的行数，列数，以及需要回答的询问数。

接下来 $Q$ 行，包含一个字母 $T$，代表棋子种类，以及两个整数 $c_1,c_R$，代表起点为第 $1$ 行的第 $c_1$ 列，终点为第 $R$ 行的第 $c_R$ 列。

各字母与棋子种类对应关系如下所示：

输出格式

对于每个询问，输出两个整数，第一个整数代表从起点到终点需要走的最少步数，第二个整数代表在步数最少的前提下，从起点到终点的方案数。

因为方案数可能很大，请输出其对 $10^9+7$ 取模后的结果。

特别地，若无法从起点到达终点，请输出一行 0 0。

8 8 5
P 1 2
R 4 8
Q 2 3
B 3 6
K 5 5

0 0
2 2
2 5
2 2
7 393

提示

所有测试点均满足：$1 \leq Q \leq 1000$，$2 \leq C \leq 1000$，$C \leq R \leq 10^9$，$T \in \{\texttt{P},\texttt{R},\texttt{Q},\texttt{B},\texttt{K}\}$，$1 \leq c_1,c_R \leq C$。

各子任务的约束条件如下：