题目背景

博丽灵梦有一块好大好大的阴阳玉，它是是博丽灵梦的主要武器之一。

但是阴阳玉的能量来源，源自主人的灵力聚集力量，因此，灵梦在平时总是需要对其进行保养。简单来说，灵梦会使用灵力，来获取阴阳玉所需的能量。

题目描述

灵力有阴阳之分。初始的时候，灵梦只有两个阳灵力，它们围成了一个圈。每次，灵梦可以进行以下两种操作：

• 在两个灵力直接加入一个阳灵力。

• 移走一个阳灵力。

为了保持稳定，任何时候这个圈上的灵力都不应该少于两个。

由于灵力的阴阳并不稳定，因此一旦某个灵力周围发生改变（多出一个灵力，或减少一个灵力），它就会从阳变成阴，或从阴变成阳。不过，如果只是周边灵力的性质改变，那么它就不会发生变化。

灵梦会不断调节灵力，直到它最终变成 $n$ 个（中途可能多于 $n$ 个）。然后，灵梦会从某个点依次按照顺时针或逆时针取下每个灵力。它会形成一条链。灵梦会用链上的能量，来加强她的阴阳玉。

做到这一点非常容易。但是灵梦非常好奇，一共可能形成多少种不同的链。

由于灵梦的偏好，她可能会有 $m$ 个限制条件。第 $i$ 个条件 $(p_i,c_i)$ ，规定了链上第 $p_i$ 个灵力应该为何种灵力。若 $c_i=0$ ，则应该为阴灵力；否则为阳。

由于可能结果太大，灵梦只需要得到答案对 $998244353$ 取模的结果。

两个链不同，当且仅当存在一个位置的点颜色不同。

输入格式

第一行为一个正整数 $n$ 和一个非负整数 $m$ 。

当 $m=0$ 时无约束条件。否则接下来会有 $m$ 行，每行两个非负整数 $p_i,c_i$ ，含义如上。

输出格式

一行，一个非负整数，表示所有链的可能种类总数对 $998244353$ 取模的值。

4 0

5

4 1
1 1

3

20 10
5 1
12 0
17 0
3 1
7 1
13 0
8 1
18 1
2 1
19 0

344

提示

样例解释

对于样例一，可能存在以下两种构造方式：

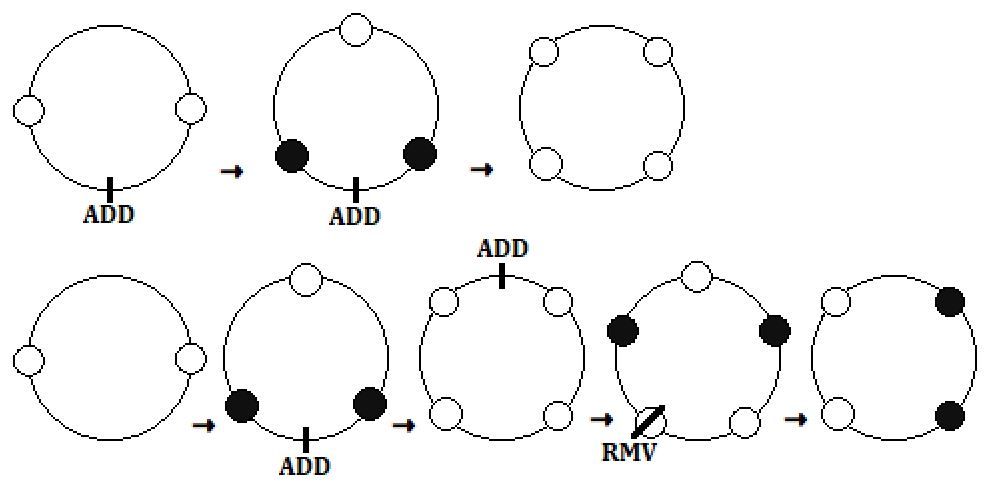
其中， $\tt ADD$ 表示增加一个阳灵力，$\tt RMV$ 表示移走一个阳灵力。

将得到的两个环分别拆开，一共可以得到以下五种链：

• 环一：阳—阳—阳—阳。

• 环二：阳—阳—阴—阴，阳—阴—阴—阳，阴—阴—阳—阳，阴—阳—阳—阴。

因此答案为 $5$ 。

对于样例二，我们限定了链上第一个灵力为阳。因此结果为 $3$ 。

数据范围

$$\def{\t}{\text}\def\arraystretch{1.5} \begin{array}{|c|c|c|c|}\hline \textbf{Subtask} & n\t{ 的范围} & m\t{ 的范围} & \t{分值}\cr\hline 1 & n\le 16 & m\le 16 & 15 \cr \hline 2 & n\le 10^6 & m\le 5\times 10^3 & 40 \cr \hline 3 & n\le 10^{18} & m=0 & 15 \cr \hline 4 & n\le 10^{18} & m\le 5\times 10^3 & 30 \cr \hline \end{array}$$

此外，对于全部数据，有 $1\le p_i\le n,c_i\in \{0,1\}, 0\le m\le n$ 且 $p_i$ 各不相同。