题目背景

小 L、小 W 和小 H 在一起van♂游戏。

由于小 L 太菜了所以导致他一直在看着小 W 和小 H 打游戏。

题目描述

这款游戏的地图可以抽象成一张有 $n$ 行 $m$ 列的网格图，网格图上有 $k$ 个障碍点，相邻两点间边长为 $1$。游戏开始时小 L、小 W 和小 H 会各自随机出生在一个点。当然，他们不会出生在障碍点。

经常开局死的小 L 看着小 W 和小 H 每次在地图上汇合时经过的路径，很想知道他们每次出生后两个人之间的期望距离。（这里的距离指两点间曼哈顿距离，即 $\left|x_1-x_2\right|+\left|y_1-y_2\right|$）

由于小 L 可以非常容易算出有多少种出生点安排方案，所以你实际上只需要告诉他所有情况中他们两人距离之和。

注意：小 W 出生在点 $A$，小 H 出生在点 $B$，跟小 W 出生在点 $B$，小 H 出生在点 $A$，这两种情况视作同一种情况。

输入格式

第一行有三个整数 $n,m,k$，分别表示地图行数、列数以及障碍物点数。

接下来有 $k$ 行，第 $i$ 行有两个正整数 $x_i,y_i$，表示第 $i$ 个障碍物的位置。

输出格式

一个整数，表示所有情况中小 W 和小 H 两人出生点距离之和。

由于小 L 十分无聊，所以他让你将答案对 $10^9+7$ 取模。

3 3 2
2 1
3 3

42

9 8 8
3 2
4 6
7 3
9 5
3 7
2 2
1 6
6 4

11552

提示

对于样例一，地图样式如下（其中蓝点为障碍点，红点为可能的出生点）：

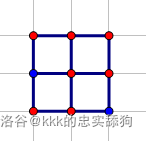
• 出生点为 $(1,1)$ 和 $(1,1)$，距离为 $0$。
• 出生点为 $(1,1)$ 和 $(1,2)$，距离为 $1$。
• 出生点为 $(1,1)$ 和 $(1,3)$，距离为 $2$。
• 出生点为 $(1,1)$ 和 $(2,2)$，距离为 $2$。
• 出生点为 $(1,1)$ 和 $(2,3)$，距离为 $3$。
• 出生点为 $(1,1)$ 和 $(3,1)$，距离为 $2$。
• 出生点为 $(1,1)$ 和 $(3,2)$，距离为 $3$。
• 出生点为 $(1,2)$ 和 $(1,2)$，距离为 $0$。
• 出生点为 $(1,2)$ 和 $(1,3)$，距离为 $1$。
• 出生点为 $(1,2)$ 和 $(2,2)$，距离为 $1$。
• 出生点为 $(1,2)$ 和 $(2,3)$，距离为 $2$。
• 出生点为 $(1,2)$ 和 $(3,1)$，距离为 $3$。
• 出生点为 $(1,2)$ 和 $(3,2)$，距离为 $2$。
• 出生点为 $(1,3)$ 和 $(1,3)$，距离为 $0$。
• 出生点为 $(1,3)$ 和 $(2,2)$，距离为 $2$。
• 出生点为 $(1,3)$ 和 $(2,3)$，距离为 $1$。
• 出生点为 $(1,3)$ 和 $(3,1)$，距离为 $4$。
• 出生点为 $(1,3)$ 和 $(3,2)$，距离为 $3$。
• 出生点为 $(2,2)$ 和 $(2,2)$，距离为 $0$。
• 出生点为 $(2,2)$ 和 $(2,3)$，距离为 $1$。
• 出生点为 $(2,2)$ 和 $(3,1)$，距离为 $2$。
• 出生点为 $(2,2)$ 和 $(3,2)$，距离为 $1$。
• 出生点为 $(2,3)$ 和 $(2,3)$，距离为 $0$。
• 出生点为 $(2,3)$ 和 $(3,1)$，距离为 $3$。
• 出生点为 $(2,3)$ 和 $(3,2)$，距离为 $2$。
• 出生点为 $(3,1)$ 和 $(3,1)$，距离为 $0$。
• 出生点为 $(3,1)$ 和 $(3,2)$，距离为 $1$。
• 出生点为 $(3,2)$ 和 $(3,2)$，距离为 $0$。

总和为 $42$。

数据范围

本题采用捆绑测试。

• Subtask 1( $10\%$ )：$n,m\leq 80$。
• Subtask 2( $20\%$ )：$n,m\leq 5000$。
• Subtask 3( $15\%$ )：$k=0$。
• Subtask 4( $15\%$ )：$m=1$。
• Subtask 5( $40\%$ )：无特殊限制。

对于 $100\%$ 的数据，$1\leq n,m\leq 10^9,1\leq x_i\leq n,1\leq y_i\leq m,0\leq k\leq 5\times 10^5,k<n\times m$，保证所有障碍点各不相同。