#P6653. [YsOI2020] 造林
[YsOI2020] 造林
Description
为了落实环保工作,Ysuperman 购进了一批树,它们都长一个样。由于树还没有种下去,所以这些树还没有根,可以认为是无根树。
Ysuperman 觉得全都种长得一样的树太无聊了,于是 TA 请到了园艺公司帮 TA 规划。园艺公司提供给了 TA 一个方法——「嫁接」。
下面给出「嫁接」操作的定义:
定义「叶子节点」为树上度数为 的节点。
「嫁接」操作指:在一棵无根树上接入一个新的「叶子节点」。
例如:
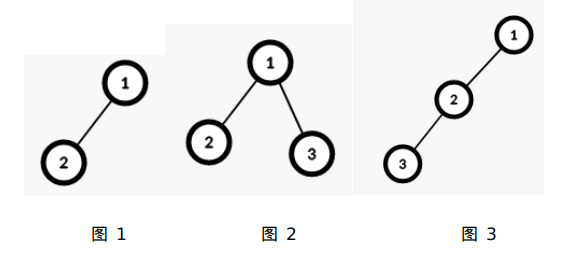
图 2 是由图 1 的树进行一次合法的嫁接操作后得到的树,图 3 也是由图 1 的树进行一次合法的嫁接操作后得到的树。
那么,我们还知道,树有一个基本属性:「品种」。
一棵树的「品种」是指每个点的最大子树大小所构成的可重集。
两棵树的「品种」不同,当且仅当每个点的最大子树大小所构成的可重集不同。
这里的一个点的最大子树大小指将这个点删掉后最大的联通块所包含的点数。
例如:
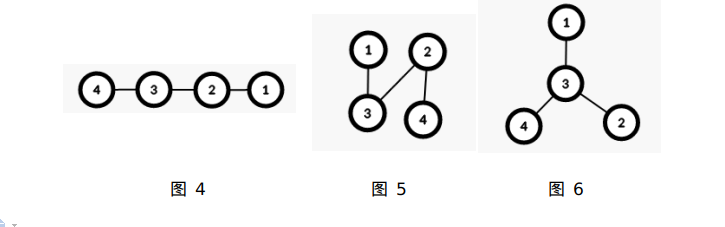
图 4 的树的每个点的最大子树大小所构成的可重集为:
图 5 的树的每个点的最大子树大小所构成的可重集为:
图 6 的树的每个点的最大子树大小所构成的可重集为:
所以说,图 4 的树与图 5 的树「品种」相同,与图 6 的树「品种」不同。
Ysuperman 想知道,通过一次「嫁接」操作,可以构造出的树包含多少不同的「品种」,以及对于每个「品种」,有多少不同的「嫁接」方法可以构造。请从小到大输出每个「品种」的「嫁接」方法数。
两个「嫁接」方案不同,当且仅当在「嫁接」操作中与新接入的「叶子节点」直接相连的点不同。
Input Format
第一行一个数 。
接下来 行,每行两个数 表示 之间有一条无向边。
Output Format
第一行一个数 ,表示可以构造出的树包含多少不同的「品种」。
第二行到第 行,从小到大输出每个「品种」的「嫁接」方法数。
5
1 2
2 3
3 4
4 5
3
1
2
2
7
1 2
1 3
2 4
2 5
3 6
3 7
3
1
2
4
25
15 9
22 15
23 22
25 15
13 23
6 22
12 15
1 23
19 13
18 9
11 15
17 1
4 25
3 1
8 9
20 1
10 18
21 20
16 8
2 22
24 1
7 19
5 16
14 7
17
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
3
Hint
本题采用捆绑测试。
样例解释 1
可以构造出 1 种「品种」为 的树。
可以构造出 2 种「品种」为 的树。
可以构造出 2 种「品种」为 的树。
样例解释 2
可以构造出 1 种「品种」为 的树。
可以构造出 2 种「品种」为 的树。
可以构造出 4 种「品种」为 的树。
对于 100% 的数据,满足 。
定义「链」为所有节点度数不超过 的树。
定义「菊花」为包含 个「叶子节点」的树。
特殊性质 1:保证树的形态为一条「链」。
特殊性质 2:保证树的形态为一朵「菊花」。
特殊性质 3:保证树的形态为一棵完全二叉树。
| subtask | 特殊性质 | 分值 | 时间限制 | |
|---|---|---|---|---|
| 1 | 2 | 4s | ||
| 2 | 1 | 3 | ||
| 3 | 无 | 5 | 1s | |
| 4 | 3 | 7 | 4s | |
| 5 | 无 | 23 | 1s | |
| 6 | 29 | 2s | ||
| 7 | 31 | 4s | ||
提示:
如果你不知道完全二叉树是什么意思,Ysuperman 提供了一个链接:Link。
输入输出较大,请使用较快的输入输出方式。
如果您使用了所需栈空间较大的递归算法,可以在本地(NOI linux 下)先使用 sudo su 获取权限,再使用 ulimit -s unlimited 命令开启无限栈。
题目并不难。

 京公网安备 11011102002149号
京公网安备 11011102002149号