#P6383. 『MdOI R2』Resurrection
『MdOI R2』Resurrection
Description
有一棵包含 个节点的树 ,它的所有边依次编号为 至 。
保证对于 中任意一个节点 ,从 到 号节点的简单路径都不经过任何编号小于 的节点。
按照如下步骤生成一张包含 个节点的无向图 :
选取一个 的排列 ,然后依次进行 次操作。在进行第 次操作时,首先删除树 中编号为 的边 ,然后,记 和 分别为当前树 中与 联通的所有点中,编号最大的点,并在图 的 号点和 号点之间连一条边。
求对于给定的树 ,按上述方式一共可以生成多少种本质不同的图 。图 和 本质不同当且仅当存在 和 满足在 中不存在边 ,而 中存在。
因为答案可能很大,你只需要求出答案对 取模的值。
Input Format
第一行一个整数 ,表示树 中的节点数量。
接下来 行,第 行两个整数 ,表示在 中编号为 的边是 。
Output Format
一行一个整数,答案对 取模的值。
4
1 4
2 3
3 4
2
11
1 4
2 6
3 11
4 6
5 6
6 7
7 9
8 9
9 10
10 11
4605
Hint
【帮助与提示】
为方便选手测试代码,本题额外提供一组附加样例供选手使用。
【样例解释】
样例一中可能生成的图 如图所示:
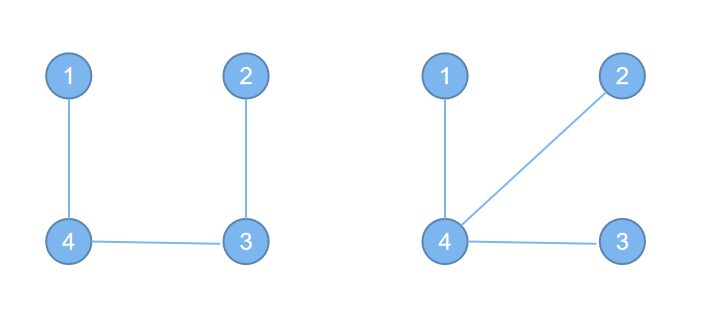
当 时将生成右侧的图,否则将生成左侧的图。
对于样例二,我有一个绝妙的解释,只可惜这里空白的位置太小,写不下。
【数据范围】
本题采用捆绑测试。
对于全部数据,保证 ,。
保证,输入的边形成一棵树,且对于任意一个节点 ,从 到 号节点的简单路径都不经过任何编号小于 的节点。
| 子任务编号 | 特殊性质 | 分值 | |
|---|---|---|---|
| Subtask 1 | 无 | ||
| Subtask 2 | |||
| Subtask 3 | 所有节点都与 号点直接相连 | ||
| Subtask 4 | 树的形态是一条链 | ||
| Subtask 5 | 无 | ||
| Subtask 6 |
下面是本题用到的一些定义:
-
一棵树是一张有 个节点, 条边的无向连通图。
-
边 表示连接点 和点 的一条边。
-
一条路径是一个序列 ,满足对于任意 ,边 都存在于 中,且 没有被之前的操作删除。
-
点 和 联通当且仅当存在一条路径 满足 且 。任何一个点都和自己联通。

 京公网安备 11011102002149号
京公网安备 11011102002149号